题目内容
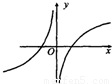
函数y=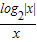 的图象大致是( )
的图象大致是( )A.
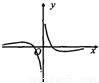
B.
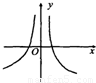
C.
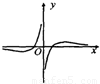
D.
【答案】分析:函数为奇函数,首先作出函数y=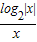 在区间[0,+∞)上的图象,由于函数图象关于原点对称,得出图象.
在区间[0,+∞)上的图象,由于函数图象关于原点对称,得出图象.
解答: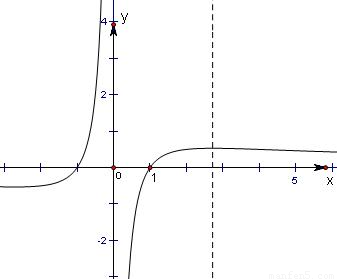 解:由于
解:由于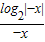 =
=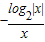 ,
,
∴函数y=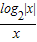 是奇函数,其图象关于原点对称.
是奇函数,其图象关于原点对称.
又y′=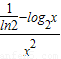 ,由y′=0得x=
,由y′=0得x=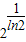
当0<x<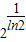 时,y′>0,当x>
时,y′>0,当x>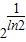 时,y′<0,
时,y′<0,
∴原函数在(0,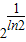 )上是增函数,在(
)上是增函数,在(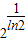 ,+∞)上是减函数,
,+∞)上是减函数,
首先作出函数y=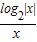 在区间(0,+∞)上的图象,由于此函数为奇函数,所以在(-∞,0)上的图象与函数在[0,+∝)上的图象关于原点对称.
在区间(0,+∞)上的图象,由于此函数为奇函数,所以在(-∞,0)上的图象与函数在[0,+∝)上的图象关于原点对称.
故选C.
点评:本题考查对数函数的图象,要求学生能熟练运用对数函数的有关性质.
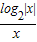 在区间[0,+∞)上的图象,由于函数图象关于原点对称,得出图象.
在区间[0,+∞)上的图象,由于函数图象关于原点对称,得出图象.解答:
 解:由于
解:由于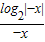 =
=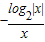 ,
,∴函数y=
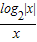 是奇函数,其图象关于原点对称.
是奇函数,其图象关于原点对称.又y′=
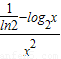 ,由y′=0得x=
,由y′=0得x=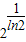
当0<x<
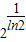 时,y′>0,当x>
时,y′>0,当x>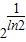 时,y′<0,
时,y′<0,∴原函数在(0,
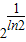 )上是增函数,在(
)上是增函数,在(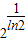 ,+∞)上是减函数,
,+∞)上是减函数,首先作出函数y=
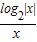 在区间(0,+∞)上的图象,由于此函数为奇函数,所以在(-∞,0)上的图象与函数在[0,+∝)上的图象关于原点对称.
在区间(0,+∞)上的图象,由于此函数为奇函数,所以在(-∞,0)上的图象与函数在[0,+∝)上的图象关于原点对称.故选C.
点评:本题考查对数函数的图象,要求学生能熟练运用对数函数的有关性质.

练习册系列答案
相关题目



 的图象大致是( )
的图象大致是( )



 的图象大致是( )
的图象大致是( )


