题目内容
13.正四棱锥S-ABCD的底面边长为4,高为3,E是边BC的中点,动点P在表面上运动,并且总保持PE⊥AC,则动点P的轨迹的周长为2$\sqrt{2}$+$\sqrt{17}$.分析 由题意知:点P的轨迹为如图所示的三角形EFG,其中G、F为中点,可得EF=$\frac{1}{2}$BD,GE=GF=$\frac{1}{2}$SB,即可得出.
解答 解:由题意知:点P的轨迹为如图所示的三角形EFG,
其中G、F为中点,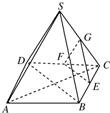 BD=4$\sqrt{2}$,SB=$\sqrt{{3}^{2}+(2\sqrt{2})^{2}}$=$\sqrt{17}$.
BD=4$\sqrt{2}$,SB=$\sqrt{{3}^{2}+(2\sqrt{2})^{2}}$=$\sqrt{17}$.
∴EF=$\frac{1}{2}$BD=2$\sqrt{2}$,
GE=GF=$\frac{1}{2}$SB=$\frac{\sqrt{17}}{2}$,
∴轨迹的周长为2$\sqrt{2}$+$\sqrt{17}$.
故答案为:2$\sqrt{2}$+$\sqrt{17}$.
点评 本题考查了正四棱锥的性质、三角形中位线定理、勾股定理、正方形的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
8.已知集合P={0,x},Q={lnx,2},P∩Q={0},则P∪Q为( )
| A. | {0,2} | B. | {0,1,2} | C. | {1,2} | D. | {0,1} |
2.运行如图的程序,若x=2,则输出的y等于( )


| A. | 9 | B. | 7 | C. | 13 | D. | 11 |
3.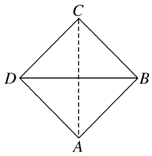 已知正四面体(所有棱长都相等的三棱锥)的俯视图如图所示,其中四边形ABCD是边长为$\sqrt{2}$cm的正方形,则这个正四面体的主视图的面积为( )cm2.
已知正四面体(所有棱长都相等的三棱锥)的俯视图如图所示,其中四边形ABCD是边长为$\sqrt{2}$cm的正方形,则这个正四面体的主视图的面积为( )cm2.
 已知正四面体(所有棱长都相等的三棱锥)的俯视图如图所示,其中四边形ABCD是边长为$\sqrt{2}$cm的正方形,则这个正四面体的主视图的面积为( )cm2.
已知正四面体(所有棱长都相等的三棱锥)的俯视图如图所示,其中四边形ABCD是边长为$\sqrt{2}$cm的正方形,则这个正四面体的主视图的面积为( )cm2.| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 2$\sqrt{2}$ |