题目内容
已知f′(x)g(x)-f(x)g′(x)=x2(1-x),则函数
( )
| f(x) |
| g(x) |
| A.有极大值点1,极小值点0 |
| B.有极大值点0,极小值点1 |
| C.有极大值点1,无极小值点 |
| D.有极小值点0,无极大值点 |
构造函数F(x)=
,则由商的导数,可得F′(x)=
=
令F′(x)=0,即
=0,解得,x=0,或x=1.
并且当x<0时,F′(x)>0,0<x<1时,F′(x)>0,由极值的定义可知,即x=0不是函数F(x)的极值点;
同理,可得当x>1时,F′(x)<0,由极值的定义可知,x=1是函数F(x)的极大值点.
故选C
| f(x) |
| g(x) |
| f′(x)g(x)-f(x)g′(x) |
| [g(x)]2 |
| x2(1-x) |
| [g(x)]2 |
令F′(x)=0,即
| x2(1-x) |
| [g(x)]2 |
并且当x<0时,F′(x)>0,0<x<1时,F′(x)>0,由极值的定义可知,即x=0不是函数F(x)的极值点;
同理,可得当x>1时,F′(x)<0,由极值的定义可知,x=1是函数F(x)的极大值点.
故选C

练习册系列答案
相关题目
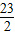 对任意n∈N*和任意实数x均成立,若存在求出满足条件的所有自然数M.
对任意n∈N*和任意实数x均成立,若存在求出满足条件的所有自然数M.