题目内容
解关于x的不等式:ax2+(a-1)x-1<0,其中a≤0.
【答案】分析:通过对a分类讨论和利用一元二次不等式的解法即可得出.
解答:解:ax2+(a-1)x-1<0,其中a≤0,化为(ax-1)(x+1)<0.
当a=0时,化为-x-1<0,解得x>-1.
当-′1<a<0时,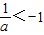 ,化为
,化为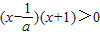 ,解得
,解得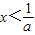 或x>-1.
或x>-1.
当a=-1时,化为(-x-1)(x+1)<0,解得x≠-1.
当a<-1时,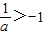 ,化为
,化为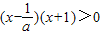 ,解得x<-1或
,解得x<-1或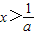 .
.
综上:当a=0时,原不等式的解集为{x|x>-1};
当-1≤a<0时,原不等式的解集为{x|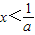 或x>-1};
或x>-1};
当a<-1时,原不等式的解集为{x|x<-1或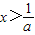 }.
}.
点评:熟练掌握一元二次不等式的解法和分类讨论的思想方法等是解题的关键.
解答:解:ax2+(a-1)x-1<0,其中a≤0,化为(ax-1)(x+1)<0.
当a=0时,化为-x-1<0,解得x>-1.
当-′1<a<0时,
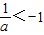 ,化为
,化为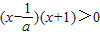 ,解得
,解得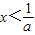 或x>-1.
或x>-1.当a=-1时,化为(-x-1)(x+1)<0,解得x≠-1.
当a<-1时,
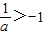 ,化为
,化为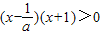 ,解得x<-1或
,解得x<-1或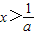 .
.综上:当a=0时,原不等式的解集为{x|x>-1};
当-1≤a<0时,原不等式的解集为{x|
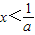 或x>-1};
或x>-1};当a<-1时,原不等式的解集为{x|x<-1或
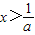 }.
}.点评:熟练掌握一元二次不等式的解法和分类讨论的思想方法等是解题的关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目