题目内容
函数y=lnx关于直线x=1对称的函数为f(x),又函数 的导函数为g(x),记h(x)=f(x)+g(x).
的导函数为g(x),记h(x)=f(x)+g(x).(1)设曲线y=h(x)在点(1,h(1))处的切线为l,l与圆(x+1)2+y2=1相切,求a的值;
(2)求函数h(x)的单调区间;
(3)求函数h(x)在[0,1]上的最大值.
【答案】分析:(1)先求过(1,h(1))点的切线方程,根据l与圆(x+1)2+y2=1相切,利用点线距离等于半径可求a的值;
(2)先求导函数,结合函数的定义域,利用导数大于0的函数的单调增区间,导数小于0得函数的单调减区间
(3)根据(2)中函数的单调区间,结合区间[0,1]进行分类讨论,从而可求h(x)的最大值.
解答:解:(1)由题意得f(x)=ln(2-x),g(x)=ax,
∴h(x)=ln(2-x)+ax.
∴ ,过(1,h(1))点的直线的斜率为a-1,
,过(1,h(1))点的直线的斜率为a-1,
∴过(1,h(1))点的直线方程为y-a=(a-1)(x-1).
又已知圆心为(-1,0),半径为1,
由题意得 ,解得a=1.
,解得a=1.
(2) .
.
∵a>0,∴ .
.
令h′(x)>0,∴ ;
;
令h′(x)<0,∴ ,
,
所以, 是h(x)的增区间,
是h(x)的增区间, 是h(x)的减区间.
是h(x)的减区间.
(3)①当 ,即
,即 时,h(x)在[0,1]上是减函数,
时,h(x)在[0,1]上是减函数,
∴h(x)的最大值为h(0)=ln2.
②当 ,即
,即 时,,h(x)在
时,,h(x)在 上是增函数,在
上是增函数,在 上是减函数,
上是减函数,
∴当 时,h(x)的最大值为
时,h(x)的最大值为 .
.
③当 ,即a≥1时,h(x)在[0,1]上是增函数,
,即a≥1时,h(x)在[0,1]上是增函数,
∴h(x)的最大值为h(1)=a.
综上,当 时,h(x)的最大值为ln2;
时,h(x)的最大值为ln2;
当 时,h(x)的最大值为2a-1-lna;
时,h(x)的最大值为2a-1-lna;
当a≥1时,h(x)的最大值为a.
点评:本题以函数为载体,考查导数的几何意义,考查利用导数求函数的单调区间与最值,分类讨论是解题的关键与难点.
(2)先求导函数,结合函数的定义域,利用导数大于0的函数的单调增区间,导数小于0得函数的单调减区间
(3)根据(2)中函数的单调区间,结合区间[0,1]进行分类讨论,从而可求h(x)的最大值.
解答:解:(1)由题意得f(x)=ln(2-x),g(x)=ax,
∴h(x)=ln(2-x)+ax.
∴
 ,过(1,h(1))点的直线的斜率为a-1,
,过(1,h(1))点的直线的斜率为a-1,∴过(1,h(1))点的直线方程为y-a=(a-1)(x-1).
又已知圆心为(-1,0),半径为1,
由题意得
 ,解得a=1.
,解得a=1.(2)
 .
.∵a>0,∴
 .
.令h′(x)>0,∴
 ;
;令h′(x)<0,∴
 ,
,所以,
 是h(x)的增区间,
是h(x)的增区间, 是h(x)的减区间.
是h(x)的减区间.(3)①当
 ,即
,即 时,h(x)在[0,1]上是减函数,
时,h(x)在[0,1]上是减函数,∴h(x)的最大值为h(0)=ln2.
②当
 ,即
,即 时,,h(x)在
时,,h(x)在 上是增函数,在
上是增函数,在 上是减函数,
上是减函数,∴当
 时,h(x)的最大值为
时,h(x)的最大值为 .
.③当
 ,即a≥1时,h(x)在[0,1]上是增函数,
,即a≥1时,h(x)在[0,1]上是增函数,∴h(x)的最大值为h(1)=a.
综上,当
 时,h(x)的最大值为ln2;
时,h(x)的最大值为ln2;当
 时,h(x)的最大值为2a-1-lna;
时,h(x)的最大值为2a-1-lna;当a≥1时,h(x)的最大值为a.
点评:本题以函数为载体,考查导数的几何意义,考查利用导数求函数的单调区间与最值,分类讨论是解题的关键与难点.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
如果将函数y=sin(2x+
)的图象向右平移φ(φ>0)个单位,所得的函数图象关于直线x=
对称,则φ的最小值为( )
| π |
| 3 |
| π |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
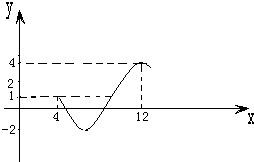 如图为函数y=Asin(ωx+φ)+c(A>0,ω>0,φ>0)图象的一部分.
如图为函数y=Asin(ωx+φ)+c(A>0,ω>0,φ>0)图象的一部分. 如图为函数y=Asin(ωx+φ)的一段图象.
如图为函数y=Asin(ωx+φ)的一段图象.