题目内容
(极坐标和参数方程4-4)极坐标系中,质点P自极点出发作直线运动到达圆: 的圆心位置后顺时针方向旋转60o后直线方向到达圆周
的圆心位置后顺时针方向旋转60o后直线方向到达圆周 上,此时P点的极坐标为 ;
上,此时P点的极坐标为 ;
(2 ,
, ).
).
解析试题分析:圆半径为2.如图所示,因为质点P自极点O出发作直线运动到达圆: 的圆心位置C后顺时针方向旋转60o后直线方向到达圆周
的圆心位置C后顺时针方向旋转60o后直线方向到达圆周 上点B,由三角形外角定理得
上点B,由三角形外角定理得 COB=
COB= CBO=
CBO=  ,在三角形OBC中,|OB|=2×
,在三角形OBC中,|OB|=2× =2
=2 ,所以P点的极坐标为(2
,所以P点的极坐标为(2 ,
, )
)
考点:本题主要考查极坐标及常见曲线的极坐标方程。
点评:简单题,利用几何图形的特殊性,借助于三角形外角定理,直角三角形边角关系等,确定点的极角、极径。

练习册系列答案
相关题目
 (
( 为参数),以直角坐标系的原点为极点,
为参数),以直角坐标系的原点为极点,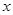 轴的正半轴为极轴,并取相同的长度单位建立极坐标系,则曲线C的极坐标方程是 .
轴的正半轴为极轴,并取相同的长度单位建立极坐标系,则曲线C的极坐标方程是 . 中,圆
中,圆 的参数方程为
的参数方程为
 为参数,
为参数, .以
.以 为极点,
为极点, 轴正半轴为极轴,并取相同的单位长度建立极坐标系,直线
轴正半轴为极轴,并取相同的单位长度建立极坐标系,直线 的极坐标方程为
的极坐标方程为 .当圆
.当圆 时,圆的半径
时,圆的半径 .
. 分别是曲线
分别是曲线 和
和 上的动点,则
上的动点,则 ,则点(2,
,则点(2, )到这条直线的距离为
)到这条直线的距离为  的极坐标方程为
的极坐标方程为 ,写出曲线
,写出曲线 与直线
与直线 相切,则实数
相切,则实数 =____________
=____________ 
 的极坐标方程为
的极坐标方程为 ,则曲线
,则曲线