题目内容
(1)证明:![]() 到直线
到直线![]() 的距离公式为
的距离公式为![]() .
.
(2)已知:在空间直角坐标系中,三元一次方程![]() (其中
(其中![]() 为常数,且
为常数,且![]() 不全为零)表示平面,
不全为零)表示平面,![]() 为该平面的一个法向量.请类比点到直线的距离公式,写出空间的点
为该平面的一个法向量.请类比点到直线的距离公式,写出空间的点![]() 到平面
到平面![]() 的距离公式,并为加以证明.
的距离公式,并为加以证明.
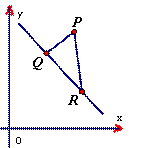 (1)证法一:设R是直线上任意一点,则R(x,y),直线的方向向量为
(1)证法一:设R是直线上任意一点,则R(x,y),直线的方向向量为![]() ,则可取直线法向量为
,则可取直线法向量为![]() ,………………2分
,………………2分
![]() ,(提醒Q不一定在直线上)……3分
,(提醒Q不一定在直线上)……3分
∴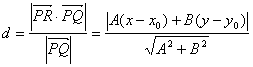
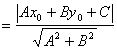 ……(6分)
……(6分)
(说明:证法一其实是求![]() 在直线的单位法向量上的投影的绝对值,借助了向量的数量积运算。)
在直线的单位法向量上的投影的绝对值,借助了向量的数量积运算。)
证法二:设A≠0,B≠0,这时![]() 与
与![]() 轴、
轴、![]() 轴都相交,过点P作
轴都相交,过点P作![]() 轴的平行线,交
轴的平行线,交![]() 于点
于点![]() ;作
;作![]() 轴的平行线,交
轴的平行线,交![]() 于点
于点![]() ,
,
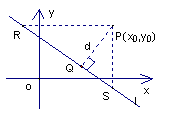 由
由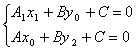 得
得![]() .
.
所以,|![]() |=|
|=|![]() |=
|=![]()
|![]() |=|
|=|![]() |=
|=![]() ……3分
……3分
|![]() |=
|=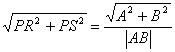 ×|
×|![]() |
|
由三角形面积公式可知:![]() ·|
·|![]() |=|
|=|![]() |·|
|·|![]() |
|
所以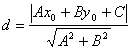
可证明,当A=0时仍适用。……6分
(2) 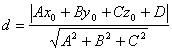 ……8分
……8分
设![]() 是平面
是平面![]() 上任意一点,因为
上任意一点,因为![]() 为该平面的一个法向量,
为该平面的一个法向量,
![]() ,
,
![]()
∴
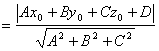 ……(13分)
……(13分)

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目