题目内容
【题目】已知数列{an}是公差为3的等差数列，数列{bn}是b1=1的等比数列，且
.
（Ⅰ）分别求数列{an}，{bn}的通项公式；
（Ⅱ）令cn= an bn，求数列{cn}的前n项和Tn.
【答案】（1）an=3n-1,bn=
,（2）Tn= 
- 
（6n+7）31-n .
【解析】
试题解析：（Ⅰ）∵anbn+1+bn+1=nbn.
当n=1时，a1b2+b2=b1.∵b1=1，b2=
， ∴a1=2，
又∵{an}是公差为3的等差数列， ∴an=3n-1，
∴
. 即
.
即数列{bn}是以1为首项，以为公比的等比数列， ∴bn=，
（Ⅱ）cn= an bn=（3n-1）
∴Tn=2×
+5×
+8×
+……+（3n-1） ①
Tn= 2×
+5×
+8×
+……+（3n-1）
②
① - ②：
Tn=2 +3×+3×……+3× -（3n-1）
=2 + 3×
-（3n-1）
∴Tn= - （6n+7）31-n .
练习册系列答案
相关题目
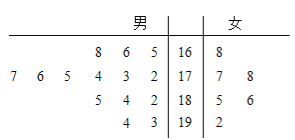
【题目】某公司2016年前三个月的利润(单位:百万元)如下:
月份 |
|
|
|
利润 |
|
|
|
（1）求利润
关于月份
的线性回归方程；
（2）试用(1)中求得的回归方程预测
月和
月的利润；
（3）试用(1)中求得的回归方程预测该公司2016年从几月份开始利润超过
万？
相关公式: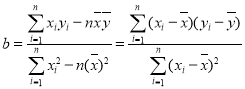 
, 
．
