题目内容
(2012•盐城一模)已知数列{an}满足a1=a(a>0,a∈N*),a1+a2+…+an-pan+1=0(p≠0,p≠-1,n∈N*).
(1)求数列{an}的通项公式an;
(2)若对每一个正整数k,若将ak+1,ak+2,ak+3按从小到大的顺序排列后,此三项均能构成等差数列,且公差为dk.
①求p的值及对应的数列{dk}.
②记Sk为数列{dk}的前k项和,问是否存在a,使得Sk<30对任意正整数k恒成立?若存在,求出a的最大值;若不存在,请说明理由.
(1)求数列{an}的通项公式an;
(2)若对每一个正整数k,若将ak+1,ak+2,ak+3按从小到大的顺序排列后,此三项均能构成等差数列,且公差为dk.
①求p的值及对应的数列{dk}.
②记Sk为数列{dk}的前k项和,问是否存在a,使得Sk<30对任意正整数k恒成立?若存在,求出a的最大值;若不存在,请说明理由.
分析:(1)因为a1+a2+…+an-pan+1=0,n≥2时,a1+a2+…+an-1-pan=0,两式相减,得
=
(n≥2),从而可知数列{an}从第二项起是公比为
的等比数列,由此可求数列{an}的通项公式an;
(2)①由(1)得ak+1=
(
)k-1,ak+2=
(
)k,ak+3=
(
)k+1,再进行分类讨论:
[1]若ak+1为等差中项,则2ak+1=ak+2+ak+3;[2]若ak+2为等差中项,则2ak+2=ak+1+ak+3,;[3]若ak+3为等差中项,则2ak+3=ak+1+ak+2,从而可求p的值及对应的数列{dk};
②分类讨论,计算Sk,利用Sk<30,建立不等式,再分离参数,由此可求满足题意的最大正整数.
| an+1 |
| an |
| p+1 |
| p |
| p+1 |
| p |
(2)①由(1)得ak+1=
| a |
| p |
| p+1 |
| p |
| a |
| p |
| p+1 |
| p |
| a |
| p |
| p+1 |
| p |
[1]若ak+1为等差中项,则2ak+1=ak+2+ak+3;[2]若ak+2为等差中项,则2ak+2=ak+1+ak+3,;[3]若ak+3为等差中项,则2ak+3=ak+1+ak+2,从而可求p的值及对应的数列{dk};
②分类讨论,计算Sk,利用Sk<30,建立不等式,再分离参数,由此可求满足题意的最大正整数.
解答:解:(1)因为a1+a2+…+an-pan+1=0,
所以n≥2时,a1+a2+…+an-1-pan=0,两式相减,得
=
(n≥2),
故数列{an}从第二项起是公比为
的等比数列…(3分)
又当n=1时,a1-pa2=0,解得a2=
,
从而an=
…(5分)
(2)①由(1)得ak+1=
(
)k-1,ak+2=
(
)k,ak+3=
(
)k+1,
[1]若ak+1为等差中项,则2ak+1=ak+2+ak+3,
即
=1或
=-2,解得p=-
…(6分)
此时ak+1=-3a(-2)k-1,ak+2=-3a(-2)k,
所以dk=|ak+1-ak+2|=9a•2k-1…(8分)
[2]若ak+2为等差中项,则2ak+2=ak+1+ak+3,即
=1,此时无解…(9分)
[3]若ak+3为等差中项,则2ak+3=ak+1+ak+2,即
=1或
=-
,解得p=-
,
此时ak+1=-
(-
)k-1,ak+3=-
(-
)k+1,
所以dk=|ak+1-ak+3|=
•(
)k-1…(11分)
综上所述,p=-
,dk=9a•2k-1或p=-
,dk=
•(
)k-1…(12分)
②[1]当p=-
时,Sk=9a(2k-1),则由Sk<30,得a<
,
当k≥3时,
<1,
所以必定有a<1,所以不存在这样的最大正整数…(14分)
[2]当p=-
时,Sk=
(1-(
)k),则由Sk<30,得a<
,
因为
>
,所以a=13满足Sk<30恒成立;但当a=14时,存在k=5,
使得a>
即Sk<30,
所以此时满足题意的最大正整数a=13…(16分)
所以n≥2时,a1+a2+…+an-1-pan=0,两式相减,得
| an+1 |
| an |
| p+1 |
| p |
故数列{an}从第二项起是公比为
| p+1 |
| p |
又当n=1时,a1-pa2=0,解得a2=
| a |
| p |
从而an=
|
|
(2)①由(1)得ak+1=
| a |
| p |
| p+1 |
| p |
| a |
| p |
| p+1 |
| p |
| a |
| p |
| p+1 |
| p |
[1]若ak+1为等差中项,则2ak+1=ak+2+ak+3,
即
| p+1 |
| p |
| p+1 |
| p |
| 1 |
| 3 |
此时ak+1=-3a(-2)k-1,ak+2=-3a(-2)k,
所以dk=|ak+1-ak+2|=9a•2k-1…(8分)
[2]若ak+2为等差中项,则2ak+2=ak+1+ak+3,即
| p+1 |
| p |
[3]若ak+3为等差中项,则2ak+3=ak+1+ak+2,即
| p+1 |
| p |
| p+1 |
| p |
| 1 |
| 2 |
| 2 |
| 3 |
此时ak+1=-
| 3a |
| 2 |
| 1 |
| 2 |
| 3a |
| 2 |
| 1 |
| 2 |
所以dk=|ak+1-ak+3|=
| 9a |
| 8 |
| 1 |
| 2 |
综上所述,p=-
| 1 |
| 3 |
| 2 |
| 3 |
| 9a |
| 8 |
| 1 |
| 2 |
②[1]当p=-
| 1 |
| 3 |
| 10 |
| 3(2k-1) |
当k≥3时,
| 10 |
| 3(2k-1) |
所以必定有a<1,所以不存在这样的最大正整数…(14分)
[2]当p=-
| 2 |
| 3 |
| 9a |
| 4 |
| 1 |
| 2 |
| 40 | ||
3(1-(
|
因为
| 40 | ||
3(1-(
|
| 40 |
| 3 |
使得a>
| 40 | ||
3(1-(
|
所以此时满足题意的最大正整数a=13…(16分)
点评:本题重点考查数列的通项与求和,考查分类讨论的数学思想,考查分离参数法的运用,综合性较强,有难度.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
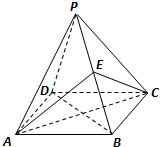 (2012•盐城一模)如图,在四棱锥P-ABCD中,四边形ABCD是菱形,PA=PC,E为PB的中点.
(2012•盐城一模)如图,在四棱锥P-ABCD中,四边形ABCD是菱形,PA=PC,E为PB的中点.