题目内容
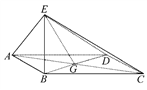
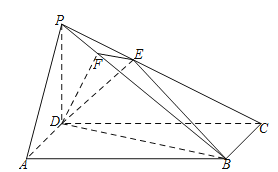
【题目】如图，在四棱锥
中，底面
是长方形，侧棱
底面，且
，过D作
于F，过F作
交 PC于E.
（Ⅰ）证明：
平面PBC；
（Ⅱ）求平面
与平面所成二面角的余弦值.
【答案】（Ⅰ）见解析; （Ⅱ）
.
【解析】【试题分析】（Ⅰ）依据题设运用直线与平面垂直的判定定理推证; （Ⅱ）依据题设条件运用二面角的平面角的定义求解或运用向量的数量积公式求解：.
解法一：（Ⅰ）因为
底面
，所以
，
由底面
为长方形，有
，而
，
所以
. 而
，所以
. ………………………2分
又因为
， 
所以
平面
. 而
，所以
. ………………………4分
又
，
，所以
平面
. ………………………6分
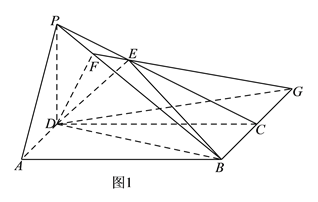
（Ⅱ）如图1，在面内，延长
与
交于点
，则
是平面与平面
的交线. 由（Ⅰ）知，
，所以
. ………………………8分
又因为
底面，所以
. 而
，所以
.
故
是面与面所成二面角的平面角， ………………………10分
在Rt△PDB中, 由 
,
故面
与面所成二面角的余弦为
. ………………………12分
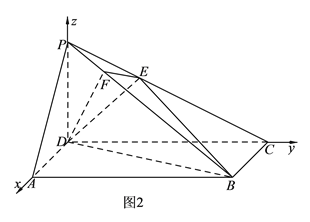
解法二：如图2, 由
，所以
是平面的一个法向量； ……………………………………8分
由（Ⅰ）知，
，所以
是平面的一个法向量 ……………………………………10分
设平面与平面所成二面角为
则
，
故面与面所成二面角的余弦为. ……………………………………12分
练习册系列答案
相关题目
