题目内容
13.二次函数f(x)满足f(x+1)-f(x)=2x,且f(0)=1.(1)求f(x)的解析式;
(2)设g(x)=2x+m,若对任意的x∈[-1,1],f(x)>g(x)恒成立,求m的取值范围.
分析 (1)利用f(0)=1,解得:c=1,由 f(x+1)-f(x)=2x.利用待定系数法求解即可.
(2)不等式 f(x)>2x+m,化为x2-3x+1-m>0.设 h(x)=x2-3x+1-m,对称轴为 x=$\frac{3}{2}$,判断h(x)在[-1,1]上是单调递减函数.然后最后求解即可.
解答 解:(1)设为f(x)=ax2+bx+c,
由题可知:f(0)=1,解得:c=1,
由 f(x+1)-f(x)=2x.可知:[a(x+1)2+b(x+1)+1]-(ax2+bx+1)=2x
化简得:2ax+a+b=2x,
所以:a=1,b=-1.∴f(x)=x2-x+1.
(2)不等式 f(x)>2x+m,可化简为 x2-x+1>2x+m
即:x2-3x+1-m>0.
设h(x)=x2-3x+1-m,则其对称轴为 x=$\frac{3}{2}$,∴h(x)在[-1,1]上是单调递减函数.
因此只需h(x)的最小值大于零即可,∴g(1)>0.
代入得:1-3+1-m>0解得:m<-1
所以实数 m的取值范围是:m<-1(备注:此题分离参数也可)
点评 本题考查二次函数的解析式的求法,函数恒成立的应用,考查转化思想以及计算能力.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
3.已知圆的方程是x2+y2=1,则经过圆上一点M(1,0)的切线方程是( )
| A. | x=1 | B. | y=1 | C. | x+y=1 | D. | x-y=1 |
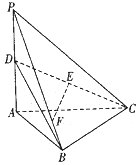 如图,三棱锥P-ABC中,PA⊥平面ABC,∠ABC=90°,PA=AC=2,D是PA的中点,E是CD的中点,点F在PB上,$\overrightarrow{PF}$=3$\overrightarrow{FB}$.
如图,三棱锥P-ABC中,PA⊥平面ABC,∠ABC=90°,PA=AC=2,D是PA的中点,E是CD的中点,点F在PB上,$\overrightarrow{PF}$=3$\overrightarrow{FB}$.