题目内容
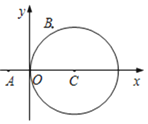
【题目】已知圆C:![]() .
.
(1)求经过点![]() 且与圆C相切的直线方程;
且与圆C相切的直线方程;
(2)设直线![]() 与圆C相交于A,B两点,若
与圆C相交于A,B两点,若![]() ,求实数n的值;
,求实数n的值;
(3)若点![]() 在以
在以![]() 为圆心,以1为半径的圆上,距离为4的两点P,Q在圆C上,求
为圆心,以1为半径的圆上,距离为4的两点P,Q在圆C上,求![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)![]()
【解析】
(1)点![]() 就在圆上,且与圆心横坐标一样,则可直接写出切线方程;
就在圆上,且与圆心横坐标一样,则可直接写出切线方程;
(2)由数量积的运算可得![]() ,则
,则![]() ,进而可得圆心到直线的距离,再由点到直线的距离可得实数n的值;
,进而可得圆心到直线的距离,再由点到直线的距离可得实数n的值;
(3)利用向量的几何运算可得![]() ,求出
,求出![]() 的最小值,即可得
的最小值,即可得![]() 最小值.
最小值.
解:(1)因为![]() ,则点
,则点![]() 就在圆C上,
就在圆C上,
故点![]() 就是切点,又圆心为
就是切点,又圆心为![]()
则切线斜率为![]() ,
,
所以经过点![]() 且与圆C相切的直线方程
且与圆C相切的直线方程![]() ;
;
(2)∵![]()
![]() ,又
,又![]() ,
,
∴![]() ,
,
则圆心到直线的距离为![]() ,
,
∴![]() 或
或![]() ;
;
(3)∵![]()
![]() ,
,
∴当NC最小时,![]() 最小,
最小,
∵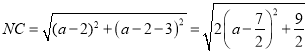 ,
,
∴当![]() 时,
时,![]() 取得最小值为
取得最小值为![]() ,
,
此时![]() 最小为
最小为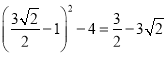 .
.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案
相关题目
【题目】某工厂因排污比较严重,决定着手整治,一个月时污染度为![]() ,整治后前四个月的污染度如下表:
,整治后前四个月的污染度如下表:
月数 |
|
|
|
| … |
污染度 |
|
|
|
| … |
污染度为![]() 后,该工厂即停止整治,污染度又开始上升,现用下列三个函数模拟从整治后第一个月开始工厂的污染模式:
后,该工厂即停止整治,污染度又开始上升,现用下列三个函数模拟从整治后第一个月开始工厂的污染模式:![]() ,
,![]() ,
,![]() ,其中
,其中![]() 表示月数,
表示月数,![]() 、
、![]() 、
、![]() 分别表示污染度.
分别表示污染度.
(1)问选用哪个函数模拟比较合理,并说明理由;
(2)若以比较合理的模拟函数预测,整治后有多少个月的污染度不超过![]() .
.