题目内容
命题 :不等式
:不等式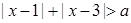 对一切实数
对一切实数 都成立;命题
都成立;命题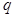 :已知函数
:已知函数 的图像在点
的图像在点 处的切线恰好与直线
处的切线恰好与直线 平行,且
平行,且 在
在 上单调递减。若命题
上单调递减。若命题 或
或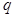 为真,求实数
为真,求实数 的取值范围。
的取值范围。
 .
.
解析试题分析:本题首先把命题 看成真命题分别求出参数
看成真命题分别求出参数 的取值范围,然后根据
的取值范围,然后根据 或
或 为真,则
为真,则 至少有一个为真便可求得实数
至少有一个为真便可求得实数 的取值范围.
的取值范围.
试题解析:由不等式 恒成立可得
恒成立可得
 真,
真,
由 得:
得:
即

令 得
得 为
为 的减区间
的减区间
依题意知:
 得
得

 或
或 为真,则
为真,则 至少有一个为真
至少有一个为真
考点:1.命题真假的判断;2.导数求单调区间.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
 :
: ,命题
,命题 :
: ,若
,若 是
是 的充分不必要条件,求实数
的充分不必要条件,求实数 的取值范围.
的取值范围. ,命题q:
,命题q: ,若
,若 为真,
为真, 为假,求实数
为假,求实数 的取值范围.
的取值范围. :方程
:方程 表示焦点在
表示焦点在 轴的椭圆;命题
轴的椭圆;命题 :关于
:关于 的不等式
的不等式 的解集是R;若“
的解集是R;若“ ” 是假命题,“
” 是假命题,“ ”是真命题,求实数
”是真命题,求实数 的取值范围。
的取值范围。 ∈R,设命题P:
∈R,设命题P: ;命题Q:函数
;命题Q:函数 有两个不同的零点.求使“P
有两个不同的零点.求使“P Q”为假命题的实数
Q”为假命题的实数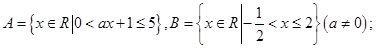
 能否相等?若能,求出实数
能否相等?若能,求出实数 的值,若不能,试说明理由?
的值,若不能,试说明理由? 命题
命题 且
且 是
是 的充分不必要条件,求实数
的充分不必要条件,求实数 。
。 ,若
,若 ,求集合A;
,求集合A;  是
是 的必要不充分条件,求
的必要不充分条件,求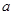 的取值范围.
的取值范围. ,设
,设 :函数
:函数 在
在 上单调递减,
上单调递减, :曲线
:曲线 与
与 轴交于不同的两点。若“
轴交于不同的两点。若“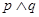 ”为假命题,“
”为假命题,“ ”为真命题,求
”为真命题,求 的取值范围。
的取值范围。 ;
; ,若
,若 是
是 的必要非充分条件,求实数
的必要非充分条件,求实数 的取值范围。
的取值范围。