题目内容
21. 设a0为常数,且an=3n-1-2an-1(n(Ⅰ)证明对任意n≥1,an=![]() [3n+(-1)n-1·2n]+(-1)n·2na0;
[3n+(-1)n-1·2n]+(-1)n·2na0;
(Ⅱ)假设对任意n≥1有an>an-1,求a0的取值范围.
21.
(Ⅰ)证法一:(ⅰ)当n=1时,由已知a1=1-
(ⅱ)假设当n=k(k≥1)等式成立,即
ak=![]() [3k+(-1)k-12k]+(-1)k2ka0,
[3k+(-1)k-12k]+(-1)k2ka0,
那么ak+1=3k-2ak
=3k-![]() [3k+(-1)k-12k]-(-1)k2k+
[3k+(-1)k-12k]-(-1)k2k+
=![]() [3k+1+(-1)k2k+1]+(-1)k+12k+
[3k+1+(-1)k2k+1]+(-1)k+12k+
也就是说,当n=k+1时,等式也成立.
根据(ⅰ)和(ⅱ),可知等式对任何n![]() N+成立.
N+成立.
证法二:如果设an-![]() 3n=-2(an-1-
3n=-2(an-1-![]() 3n-1),
3n-1),
用an=3n-1-2an-1代入,可解出![]() =
=![]() .
.
所以![]() 是公比为-2,首项为a1-
是公比为-2,首项为a1-![]() 的等比数列,
的等比数列,
∴an-![]() =(1-
=(1-![]() )(-2)n-1(n
)(-2)n-1(n![]() N+),
N+),
即an=![]() +(-1)n2na0.
+(-1)n2na0.
(Ⅱ)解法一:由an通项公式
an-an-1=![]() +(-1)n3×2n-
+(-1)n3×2n-
∴an>an-1(n![]() N+)等价于
N+)等价于
(-1)n-1(![]() )n-2(n
)n-2(n![]() N+). ①
N+). ①
(ⅰ)当n=2k-1,k=1,2,…时,①式即为
(-1)2k-2(![]() )2k-3,
)2k-3,
即为a0<![]() (
(![]() )2k-3+
)2k-3+![]() . ②
. ②
②式对k=1,2,…都成立,有a0<![]() ×(
×(![]() )-1+
)-1+![]() =
=![]() .
.
(ⅱ)当n=2k,k=1,2,…时,①式即为
(-1)2k-1(![]() )2k-2,
)2k-2,
即为a0>-![]() ×(
×(![]() )2k-2+
)2k-2+![]() . ③
. ③
③式对k=1,2,…都成立,有a0>-![]() ×
×![]() +
+![]() =0.
=0.
综上,①式对任意n![]() N+成立,有0<a0<
N+成立,有0<a0<![]() .
.
故a0的取值范围为(0,![]() ).
).
解法二:如果an>an-1(n![]() N+)成立,特别取n=1,2有
N+)成立,特别取n=1,2有
a1-a0=1-
a2-a1=
因此 0<a0<![]() .
.
下面证明当0<a0<![]() 时,对任意n
时,对任意n![]() N+,有an-an-1>0.
N+,有an-an-1>0.
由an通项公式
5(an-an-1)=2×3n-1+(-1)n-13×2n-1+(-1)n5×3×2n-
(ⅰ)当n=2k-1,k=1,2,…时,
5(an-an-1)=2×3n-1+3×2n-1-5×3×2n-
(ⅱ)当n=2k,k=1,2,…时,
5(an-an-1)=2×3n-1-3×2n-1+5×3×2n-
故a0的取值范围为(0,![]() ).
).

 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 (2012•闸北区二模)如图,P1(x1,y1),P2(x2,y2),…,Pn(xn,yn),…是曲线
(2012•闸北区二模)如图,P1(x1,y1),P2(x2,y2),…,Pn(xn,yn),…是曲线 如图,P1(x1,y1),P2(x2,y2),…,Pn(xn,yn),…是曲线
如图,P1(x1,y1),P2(x2,y2),…,Pn(xn,yn),…是曲线 上的点,A1(a1,0),A2(a2,0),…,An(an,0),…是x轴正半轴上的点,且△A0A1P1,△A1A2P2,…,△An-1AnPn,…均为斜边在x轴上的等腰直角三角形(A0为坐标原点).
上的点,A1(a1,0),A2(a2,0),…,An(an,0),…是x轴正半轴上的点,且△A0A1P1,△A1A2P2,…,△An-1AnPn,…均为斜边在x轴上的等腰直角三角形(A0为坐标原点).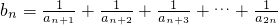 ,集合B={b1,b2,b3,…,bn,…},A={x|x2-2ax+a2-1<0,x∈R},若A∩B=∅,求实常数a的取值范围.
,集合B={b1,b2,b3,…,bn,…},A={x|x2-2ax+a2-1<0,x∈R},若A∩B=∅,求实常数a的取值范围.