题目内容
 如图,P1(x1,y1),P2(x2,y2),…,Pn(xn,yn),…是曲线
如图,P1(x1,y1),P2(x2,y2),…,Pn(xn,yn),…是曲线 上的点,A1(a1,0),A2(a2,0),…,An(an,0),…是x轴正半轴上的点,且△A0A1P1,△A1A2P2,…,△An-1AnPn,…均为斜边在x轴上的等腰直角三角形(A0为坐标原点).
上的点,A1(a1,0),A2(a2,0),…,An(an,0),…是x轴正半轴上的点,且△A0A1P1,△A1A2P2,…,△An-1AnPn,…均为斜边在x轴上的等腰直角三角形(A0为坐标原点).
(1)写出an-1、an和xn之间的等量关系,以及an-1、an和yn之间的等量关系;
(2)猜测并证明数列{an}的通项公式;
(3)设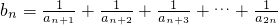 ,集合B={b1,b2,b3,…,bn,…},A={x|x2-2ax+a2-1<0,x∈R},若A∩B=∅,求实常数a的取值范围.
,集合B={b1,b2,b3,…,bn,…},A={x|x2-2ax+a2-1<0,x∈R},若A∩B=∅,求实常数a的取值范围.
解:(1)依题意利用等腰直角三角形的性质可得, ,
, .…(4分)
.…(4分)
(2)由 得
得  =
= ,
,
即 ,猜测
,猜测 . …(2分)
. …(2分)
证明:①当n=1时,可求得 ,命题成立; …(1分)
,命题成立; …(1分)
②假设当n=k时,命题成立,即有 ,…(1分)
,…(1分)
则当n=k+1时,由归纳假设及 ,
,
得 ,
,
即
解得 ,(
,( 不合题意,舍去),
不合题意,舍去),
即当n=k+1时,命题成立. …(3分)
综上所述,对所有n∈N*, . …(1分)
. …(1分)
(3)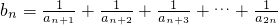 =
= =
= .…(2分)
.…(2分)
因为函数 在区间[1,+∞)上单调递增,且
在区间[1,+∞)上单调递增,且 ,
,
所以 .…(2分)
.…(2分)
A={x|x2-2ax+a2-1<0,a∈R}={x|x∈(a-1,a+1)}
由A∩B=φ,有a+1≤0,或 ,
,
故, ,即 实常数a的取值范围为
,即 实常数a的取值范围为 .…(2分)
.…(2分)
分析:(1)依题意利用等腰直角三角形的性质可得, ,
, .
.
(2)由 得
得  =
= ,即
,即 ,猜测
,猜测 ,
,
再用数学归纳法进行证明.
(3)用裂项法求得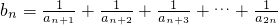 的值为
的值为 ,由函数
,由函数 在区间
在区间
[1,+∞)上单调递增,且 ,求得
,求得 ,再由 A={x|x2-2ax+a2-1<0,a∈R}=
,再由 A={x|x2-2ax+a2-1<0,a∈R}=
{x|x∈(a-1,a+1)},A∩B=φ,有a+1≤0,或 ,由此求得实常数a的取值范围.
,由此求得实常数a的取值范围.
点评:本题主要考查数学归纳法的应用,用裂项法对数列求和,两个集合的交集的定义的应用,属于难题.
 ,
, .…(4分)
.…(4分)(2)由
 得
得  =
= ,
,即
 ,猜测
,猜测 . …(2分)
. …(2分)证明:①当n=1时,可求得
 ,命题成立; …(1分)
,命题成立; …(1分)②假设当n=k时,命题成立,即有
 ,…(1分)
,…(1分)则当n=k+1时,由归纳假设及
 ,
,得
 ,
,即

解得
 ,(
,( 不合题意,舍去),
不合题意,舍去),即当n=k+1时,命题成立. …(3分)
综上所述,对所有n∈N*,
 . …(1分)
. …(1分)(3)
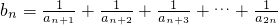 =
= =
= .…(2分)
.…(2分)因为函数
 在区间[1,+∞)上单调递增,且
在区间[1,+∞)上单调递增,且 ,
,所以
 .…(2分)
.…(2分)A={x|x2-2ax+a2-1<0,a∈R}={x|x∈(a-1,a+1)}
由A∩B=φ,有a+1≤0,或
 ,
,故,
 ,即 实常数a的取值范围为
,即 实常数a的取值范围为 .…(2分)
.…(2分)分析:(1)依题意利用等腰直角三角形的性质可得,
 ,
, .
.(2)由
 得
得  =
= ,即
,即 ,猜测
,猜测 ,
,再用数学归纳法进行证明.
(3)用裂项法求得
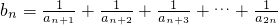 的值为
的值为 ,由函数
,由函数 在区间
在区间[1,+∞)上单调递增,且
 ,求得
,求得 ,再由 A={x|x2-2ax+a2-1<0,a∈R}=
,再由 A={x|x2-2ax+a2-1<0,a∈R}={x|x∈(a-1,a+1)},A∩B=φ,有a+1≤0,或
 ,由此求得实常数a的取值范围.
,由此求得实常数a的取值范围.点评:本题主要考查数学归纳法的应用,用裂项法对数列求和,两个集合的交集的定义的应用,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
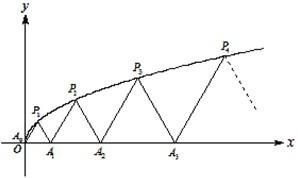 如图,P1(x1,y1)、P2(x2,y2)、…、Pn(xn,yn)(0<y1<y2<…<yn)是曲线C:y2=3x(y≥0)上的n个点,点Ai(ai,0)(i=1,2,3,…,n)在x轴的正半轴上,且△Ai-1AiPi是正三角形(A0是坐标原点).
如图,P1(x1,y1)、P2(x2,y2)、…、Pn(xn,yn)(0<y1<y2<…<yn)是曲线C:y2=3x(y≥0)上的n个点,点Ai(ai,0)(i=1,2,3,…,n)在x轴的正半轴上,且△Ai-1AiPi是正三角形(A0是坐标原点).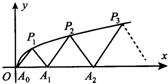 如图,P1(x1,y1),P2(x2,y2),…,Pn(xn,yn)(0<y1<y2<…<yn)是曲线C:y2=3x(y≥0)上的n个点,点Ai(ai,0)(i=1,2,3,…,n)在x轴的正半轴上,且△Ai-1AiPi是正三角形(A0是坐标原点).则a1=
如图,P1(x1,y1),P2(x2,y2),…,Pn(xn,yn)(0<y1<y2<…<yn)是曲线C:y2=3x(y≥0)上的n个点,点Ai(ai,0)(i=1,2,3,…,n)在x轴的正半轴上,且△Ai-1AiPi是正三角形(A0是坐标原点).则a1=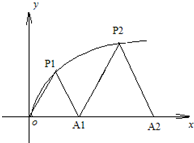 如图,P1(x1,y1)、P2(x2,y2)、…、Pn(xn,yn)(0<y1<y2<…<yn) 是曲线C:y2=3x(y≥0)上的n个点,点Ai(ai,0)(i=1,2,3,…n)在x轴的正半轴上,且△Ai-1AiPi是正三角形(A0是坐标原点).
如图,P1(x1,y1)、P2(x2,y2)、…、Pn(xn,yn)(0<y1<y2<…<yn) 是曲线C:y2=3x(y≥0)上的n个点,点Ai(ai,0)(i=1,2,3,…n)在x轴的正半轴上,且△Ai-1AiPi是正三角形(A0是坐标原点). (2012•闸北区二模)如图,P1(x1,y1),P2(x2,y2),…,Pn(xn,yn),…是曲线
(2012•闸北区二模)如图,P1(x1,y1),P2(x2,y2),…,Pn(xn,yn),…是曲线