题目内容
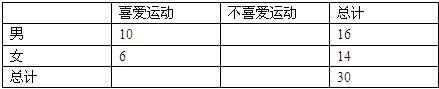
第16届亚运会将于2010年11月12日至27日在中国广州进行,为了搞好接待工作,组委会招募了16名男志愿者和14名女志愿者,调查发现,男、女志愿者中分别有10人和6人喜爱运动,其余不喜爱.(1)根据以上数据完成以下2×2列联表:

(2)根据列联表的独立性检验,能否在犯错误的概率不超过0.10的前提下认为性别与喜爱运动有关?
(3)如果从喜欢运动的女志原者中(其中恰有4人会外语),抽取2名负责翻译工作,则抽出的志愿者中2人都能胜任翻译工作的概率是多少?
参考公式:
 ,其中n=a+b+c+d.
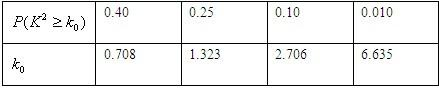
,其中n=a+b+c+d.参考数据:

【答案】分析:(1)由题中条件补充2×2列联表中的数据,
(2)利用2×2列联表中的数据,计算出k2,对性别与喜爱运动有关的程度进行判断,
(3)喜欢运动的女志愿者有6人,总数是从 这6人中挑两个人,而有4人会外语,满足条件的是从这4人中挑两个人.
解答:解:(1)
 (2分)
(2分)
(2)假设:是否喜爱运动与性别无关,由已知数据可求得:
因此,在犯错的概率不超过0.10的前提下不能判断喜爱运动与性别有关(6分)
(3)喜欢运动的女志愿者有6人,
设分别为A、B、C、D、E、F,其中A、B、C、D会外语,
则从这6人中任取2人有AB,AC,AD,AE,AF,BC,BD,
BE,BF,CD,CE,CF,DE,DF,EF,共15种取法,
其中两人都会外语的有AB,AC,AD,BC,BD,CD,共6种.
故抽出的志愿者中2人都能胜任翻译工作的概率是 (12分)
(12分)
点评:本题把概率的求法,列联表,独立性检验等知识有机的结合在一起,是一道综合性题目,但题目难度不大,符合新课标对本部分的要求,是道好题.
(2)利用2×2列联表中的数据,计算出k2,对性别与喜爱运动有关的程度进行判断,
(3)喜欢运动的女志愿者有6人,总数是从 这6人中挑两个人,而有4人会外语,满足条件的是从这4人中挑两个人.
解答:解:(1)
 (2分)
(2分)(2)假设:是否喜爱运动与性别无关,由已知数据可求得:

因此,在犯错的概率不超过0.10的前提下不能判断喜爱运动与性别有关(6分)
(3)喜欢运动的女志愿者有6人,
设分别为A、B、C、D、E、F,其中A、B、C、D会外语,
则从这6人中任取2人有AB,AC,AD,AE,AF,BC,BD,
BE,BF,CD,CE,CF,DE,DF,EF,共15种取法,
其中两人都会外语的有AB,AC,AD,BC,BD,CD,共6种.
故抽出的志愿者中2人都能胜任翻译工作的概率是
 (12分)
(12分)点评:本题把概率的求法,列联表,独立性检验等知识有机的结合在一起,是一道综合性题目,但题目难度不大,符合新课标对本部分的要求,是道好题.

练习册系列答案
相关题目
 员们正在积极备战. 若某运动员每次射击成绩为10环的概率为
员们正在积极备战. 若某运动员每次射击成绩为10环的概率为 . 求该运动员在5次射击中,(1)恰有3次射击成绩为10环的概率;
. 求该运动员在5次射击中,(1)恰有3次射击成绩为10环的概率; ,求
,求 .(结果
.(结果 用分数表示)
用分数表示)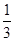 . 求该运动员在5次射击中,
. 求该运动员在5次射击中,
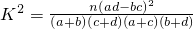 ,其中n=a+b+c+d.
,其中n=a+b+c+d.