题目内容
第16届亚运会将于2010年11月在广州市举行,射击队运动员们正在积极备战.若某运动员每次射击成绩为10环的概率为| 1 | 3 |
(1)恰有3次射击成绩为10环的概率;
(2)至少有3次射击成绩为10环的概率;
(3)记“射击成绩为10环的次数”为ξ,求Eξ.(结果用分数表示)
分析:(1)根据某运动员每次射击成绩为10环的概率为
.故该运动员在5次射击中,恰有3次射击成绩为10环的概率为
×(
)3×(1-
)2,计算后,即可得到答案.
(2)至少有3次射击成绩为10环的概率为,P(X=3)+P(X=4)+P(X=5)分别计算出P(X=3),P(X=4),P(X=5)代入即可得到答案.
(3)我们列出随机变量X的分布列,然后代入数学期望公式,即可求出答案.
| 1 |
| 3 |
| C | 3 5 |
| 1 |
| 3 |
| 1 |
| 3 |
(2)至少有3次射击成绩为10环的概率为,P(X=3)+P(X=4)+P(X=5)分别计算出P(X=3),P(X=4),P(X=5)代入即可得到答案.
(3)我们列出随机变量X的分布列,然后代入数学期望公式,即可求出答案.
解答:解:设随机变量X为射击成绩为10环的次数,则X~B(5,
).(2分)
(1)在5次射击中,恰有3次射击成绩为10环的概率为:P(x=3)=
×(
)3×(1-
)2=10×
×
=
(4分)
(2)在5次射击中,至少有3次射击成绩为10环的概率为:P(X≥3)=P(X=3)+P(X=4)+P(X=5)(6分)
=
×(
)3×(1-
)2+
×(
)4×(1-
)+
×(
)5×(1-
)0=
+
+
=
.(8分)
(3)随机变量X的分布列为:
故E(X)=0×
+1×
+2×
+3×
+4×
+5×
=
(12分)
| 1 |
| 3 |
(1)在5次射击中,恰有3次射击成绩为10环的概率为:P(x=3)=
| C | 3 5 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 27 |
| 4 |
| 9 |
| 40 |
| 243 |
(2)在5次射击中,至少有3次射击成绩为10环的概率为:P(X≥3)=P(X=3)+P(X=4)+P(X=5)(6分)
=
| C | 3 5 |
| 1 |
| 3 |
| 1 |
| 3 |
| C | 4 5 |
| 1 |
| 3 |
| 1 |
| 3 |
| C | 5 5 |
| 1 |
| 3 |
| 1 |
| 3 |
| 40 |
| 243 |
| 10 |
| 243 |
| 1 |
| 243 |
| 17 |
| 81 |
(3)随机变量X的分布列为:
| X | 0 | 1 | 2 | 3 | 4 | 5 | ||||||||||||
| P |
|
|
|
|
|
|
| 32 |
| 243 |
| 80 |
| 243 |
| 80 |
| 243 |
| 40 |
| 243 |
| 10 |
| 243 |
| 1 |
| 243 |
| 5 |
| 3 |
点评:本小题主要考查随机变量的分布列.二项分布.数学期望等知识,考查或然与必然的数学思想方法,以及数据处理能力.运算求解能力和应用意识,其中正确的分析出满足条件的基本事件,并做到不重分,不漏分是解答此类问题的关键.

练习册系列答案
相关题目
 员们正在积极备战. 若某运动员每次射击成绩为10环的概率为
员们正在积极备战. 若某运动员每次射击成绩为10环的概率为 . 求该运动员在5次射击中,(1)恰有3次射击成绩为10环的概率;
. 求该运动员在5次射击中,(1)恰有3次射击成绩为10环的概率; ,求
,求 .(结果
.(结果 用分数表示)
用分数表示)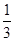 . 求该运动员在5次射击中,
. 求该运动员在5次射击中,
 ,其中n=a+b+c+d.
,其中n=a+b+c+d.