题目内容
【题目】已知函数![]() ,
,![]() 为自然对数的底数.
为自然对数的底数.
(1)求证:当![]() 时,
时,![]() ;
;
(2)若函数![]() 有两个零点,求实数
有两个零点,求实数![]() 的取值范围.
的取值范围.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)构造![]() ,再求导可得
,再求导可得![]() ,再对导数求导,继而分析导函数的正负区间进而求得原函数的单调区间求最小值证明即可.
,再对导数求导,继而分析导函数的正负区间进而求得原函数的单调区间求最小值证明即可.
(2) 求导可得![]() ,再分
,再分![]() ,
,![]() ,
,![]() 分析函数的最小值,同时根据零点存在性定理判断是否有两个零点即可.
分析函数的最小值,同时根据零点存在性定理判断是否有两个零点即可.
(1)设![]() …
…
∴![]() ,
,
∴![]()
∵![]() ∴
∴![]() ∴
∴![]()
∴![]() 在
在![]() 上单调递增,
上单调递增,
又![]()
∴![]() 时,
时,![]()
∴![]() 在
在![]() 上单调递增,
上单调递增,
又![]()
∴![]() 时,
时,![]()
故当![]() 时,
时,![]() ;
;
(2)∵![]()
∴![]() ,
,
①当![]() 时,易知函数
时,易知函数![]() 只有一个零点,不符合题意;
只有一个零点,不符合题意;
②当![]() 时,在
时,在![]() 上,
上,![]() ,
,![]() 单调递减;在
单调递减;在![]() 上,
上,![]() ,
,![]() 单调递增;又
单调递增;又![]() ,且
,且![]() ,且当
,且当![]() 上,
上,![]() 恒成立,
恒成立,
又不妨取![]() 且
且![]() 时,
时,![]()
或者考虑:当![]()
所以函数![]() 在
在![]() 和在
和在![]() 上各有一个零点,即有两个零点.
上各有一个零点,即有两个零点.
③当![]() 时,由
时,由![]() 得
得![]() 或
或![]()
(i)当![]() 即
即![]() 时,在
时,在![]() 上,
上,![]() 成立,故
成立,故![]() 在
在![]() 上单调递增,所以函数
上单调递增,所以函数![]() 至多有一个零点,不符合题意
至多有一个零点,不符合题意
(ii)当![]() 即
即![]() 时,在
时,在![]() 和
和![]() 上,
上,![]() ,
,![]() 单调递增;
单调递增;
在![]() 上
上![]() ,
,![]() 单调递减;
单调递减;
又![]() ,且
,且![]() ,
,
所以函数![]() 至多有一个零点,不符合题意
至多有一个零点,不符合题意
(iii)当![]() 即
即![]() 时,在
时,在![]() 和
和![]() 上
上![]() ,
,![]() 单调递增;在
单调递增;在![]() 上
上![]() ,
,![]() 单调递减;又
单调递减;又![]() ,所以函数
,所以函数![]() 至多有一个零点,不符合题意
至多有一个零点,不符合题意
综上所述:实数![]() 的取值范围是
的取值范围是![]()

【题目】改革开放以来,我国农村7亿多贫困人口摆脱贫困,贫困发生率由1978年的97.5%下降到2018年底的1.4%,创造了人类减贫史上的中国奇迹,为全球减贫事业贡献了中国智慧和中国方案.“贫困发生率”是指低于贫困线的人口占全体人口的比例.2012年至2018年我国贫困发生率的数据如下表:
年份( | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
贫困发生率 | 10.2 | 8.5 | 7.2 | 5.7 | 4.5 | 3.1 | 1.4 |
(1)从表中所给的7个贫困发生率数据中任选两个,求至少有一个低于5%的概率;
(2)设年份代码![]() ,利用回归方程,分析2012年至2018年贫困发生率的变化情况,并预测2019年贫困发生率.
,利用回归方程,分析2012年至2018年贫困发生率的变化情况,并预测2019年贫困发生率.
附:回归直线![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为: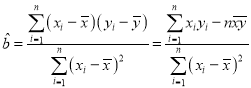 ,
,![]() .
.