题目内容
 如图,圆M与圆N交于A、B两点,以A为切点作两圆的切线分别交圆M和圆N于C、D两点,延长DB交圆M于点E,延长CB交圆N于点F,已知BC=5,BD=10,则AB=
如图,圆M与圆N交于A、B两点,以A为切点作两圆的切线分别交圆M和圆N于C、D两点,延长DB交圆M于点E,延长CB交圆N于点F,已知BC=5,BD=10,则AB=| CF | DE |
分析:由已知条件中AC,AD均为切线,结合弦切角定理,我们不难得到△ABC∽△DBA,又由已知BC=5,BD=10,可以得到一个关于AB的方程,解方程即可求出AB的值.根据切割线定理我们知道,CA2=CB•CF,DA2=DB•DE,根据△ABC∽△DBA,我们可得
的值,代入即可得到结果.
| CA |
| DA |
解答:解:根据弦切角定理,
知∠BAC=∠BDA,∠ACB=∠DAB,
故△ABC∽△DBA,
则
=
,
故AB2=BC•BD=50,AB=5
.
根据切割线定理,
知CA2=CB•CF,DA2=DB•DE,
两式相除,
得
=
•
(*).
由△ABC∽△DBA,
得
=
=
=
,
=
,
又
=
=
,
由(*)得
=1.
故答案为:5
,1
知∠BAC=∠BDA,∠ACB=∠DAB,
故△ABC∽△DBA,
则
| AB |
| DB |
| BC |
| BA |
故AB2=BC•BD=50,AB=5
| 2 |
根据切割线定理,
知CA2=CB•CF,DA2=DB•DE,
两式相除,
得
| CA2 |
| DA2 |
| CB |
| DB |
| CF |
| DE |
由△ABC∽△DBA,
得
| AC |
| DA |
| AB |
| DB |
5
| ||
| 10 |
| ||
| 2 |
| CA2 |
| DA2 |
| 1 |
| 2 |
又
| CB |
| DB |
| 5 |
| 10 |
| 1 |
| 2 |
由(*)得
| CF |
| DE |
故答案为:5
| 2 |
点评:本小题主要考查圆的切线及有关知识,如弦切角定理和切割线定理,以及分析问题与解决问题的能力、转化与化归的思想方法.在平面几何中,特别是一些定理的证明和用多个定理证明一个问题的题目,我们注意熟练掌握:1.射影定理的内容及其证明; 2.圆周角与弦切角定理的内容及其证明;3.圆幂定理的内容及其证明;4.圆内接四边形的性质与判定.

练习册系列答案
相关题目
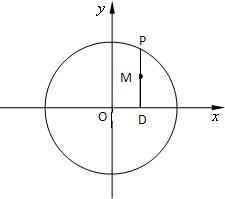 如图,P是圆x2+y2=4上的动点,P点在x轴上的投影是D,点M满足
如图,P是圆x2+y2=4上的动点,P点在x轴上的投影是D,点M满足
 的右焦点F2与抛物线y2=8x的焦点重合,过F2作与x轴垂直的直线l与椭圆交于S、T两点,与抛物线交于C、D两点,且
的右焦点F2与抛物线y2=8x的焦点重合,过F2作与x轴垂直的直线l与椭圆交于S、T两点,与抛物线交于C、D两点,且 .
. 的最大值.
的最大值.
 = .
= .