题目内容
已知函数f(x)=x-ln(x+a).(a是常数)(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)当y=f(x)在x=1处取得极值时,若关于x的方程f(x)+2x=x2+b在[0.5,2]上恰有两个不相等的实数根,求实数b的取值范围;
(Ⅲ)求证:当n≥2,n∈N+时
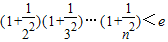 .
.
【答案】分析:(I)①求f′(x)②解不等式f′(x)>0得单增区间③f′(x)<0得单调递减区间
(II)①f'(1)=0,得a=0 f(x)=x-lnx,
②f(x)+2x=x2+b,即x-lnx+2x=x2+b,∴x2-3x+lnx+b=0,
③【0.5,2]上有两根则f(x)两次穿过x轴:g(0.5)≥0,g(1)<0,g(2)≥0可解b范围(III)由(I)和(II)可知a=0,x∈[0.5,+∞) f(x)≥f(1),即lnx≤x-1
∴x>1时,lnx<x-1令x=1+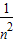 得ln(1+
得ln(1+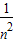 )<
)<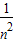 ,
,
∴n≥2,加以变形便有所求证明
解答:解:(Ⅰ)由已知由函数f(x)的定义域为x>-a,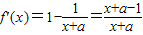 ,
,
∵-a<-a+1,
∴由f'(x)>0,得x>-a+1,
由f'(x)<0,得-a<x<-a+1,
所以函数f(x)的减区间为(-a,-a+1),增区间为(-a+1,+∞).(4分)
(II)由题意,得f'(1)=0,
∴a=0.(5分)
∴由(Ⅰ)知f(x)=x-lnx,
∴f(x)+2x=x2+b,即x-lnx+2x=x2+b,
∴x2-3x+lnx+b=0,
设g(x)=x2-3x+lnx+b(x>0),
则g'(x)=2x-3+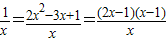
当 变化时,g'(x),g(x)的变化情况如下表:(6分)
变化时,g'(x),g(x)的变化情况如下表:(6分)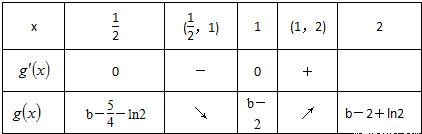
∵方程f(x)+2x=x2+b在[0.5,2]上恰有两个不相等的实数根,
∴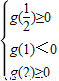 ,∴
,∴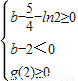 ,
,
∴ +ln2≤b<2,即
+ln2≤b<2,即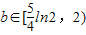 .(8分)
.(8分)
(III)由(I)和(II)可知当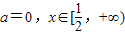 时,f(x)≥f(1),
时,f(x)≥f(1),
即lnx≤x-1,
∴当x>1时,lnx<x-1.(10分)
令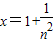 (n≥2,n∈N*),
(n≥2,n∈N*),
则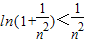 .
.
所以当n≥2,n∈N*时,
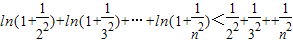
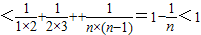 ,
,
即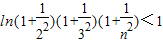 ,
,
∴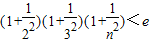 .(12分)
.(12分)
点评:本题考查导数应用求函数单调区间
(II)①f'(1)=0,得a=0 f(x)=x-lnx,
②f(x)+2x=x2+b,即x-lnx+2x=x2+b,∴x2-3x+lnx+b=0,
③【0.5,2]上有两根则f(x)两次穿过x轴:g(0.5)≥0,g(1)<0,g(2)≥0可解b范围(III)由(I)和(II)可知a=0,x∈[0.5,+∞) f(x)≥f(1),即lnx≤x-1
∴x>1时,lnx<x-1令x=1+
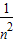 得ln(1+
得ln(1+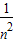 )<
)<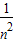 ,
,∴n≥2,加以变形便有所求证明
解答:解:(Ⅰ)由已知由函数f(x)的定义域为x>-a,
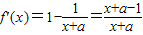 ,
,∵-a<-a+1,
∴由f'(x)>0,得x>-a+1,
由f'(x)<0,得-a<x<-a+1,
所以函数f(x)的减区间为(-a,-a+1),增区间为(-a+1,+∞).(4分)
(II)由题意,得f'(1)=0,
∴a=0.(5分)
∴由(Ⅰ)知f(x)=x-lnx,
∴f(x)+2x=x2+b,即x-lnx+2x=x2+b,
∴x2-3x+lnx+b=0,
设g(x)=x2-3x+lnx+b(x>0),
则g'(x)=2x-3+
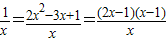
当
 变化时,g'(x),g(x)的变化情况如下表:(6分)
变化时,g'(x),g(x)的变化情况如下表:(6分)
∵方程f(x)+2x=x2+b在[0.5,2]上恰有两个不相等的实数根,
∴
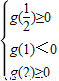 ,∴
,∴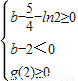 ,
,∴
 +ln2≤b<2,即
+ln2≤b<2,即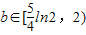 .(8分)
.(8分)(III)由(I)和(II)可知当
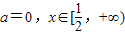 时,f(x)≥f(1),
时,f(x)≥f(1),即lnx≤x-1,
∴当x>1时,lnx<x-1.(10分)
令
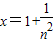 (n≥2,n∈N*),
(n≥2,n∈N*),则
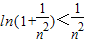 .
.所以当n≥2,n∈N*时,
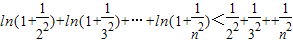
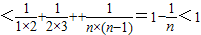 ,
,即
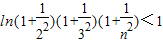 ,
,∴
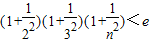 .(12分)
.(12分)点评:本题考查导数应用求函数单调区间

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|