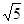题目内容
过双曲线的一个焦点F2作垂直于实轴的弦PQ，F1是另一焦点，若∠
，则双曲线的离心率e等于（ ）A．
B．
C．
D．
【答案】分析：根据由题设条件可知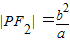
，|F1F2|=2c，由此可以求出双曲线的离心率e．
解答：解：由题意可知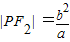
，|F1F2|=2c，
∵∠
，
∴
，
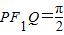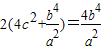∴4a2c2=b4=（c2-a2）2=c4-2a2c2+a4，
整理得e4-6e2+1=0，
解得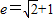
或
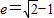（舍去）
故选C．
点评：本题考查双曲线的离心率，解题要注意时双曲线的离心率大于1．
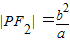，|F1F2|=2c，由此可以求出双曲线的离心率e．解答：解：由题意可知
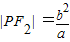，|F1F2|=2c，∵∠
，∴
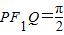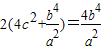，∴4a2c2=b4=（c2-a2）2=c4-2a2c2+a4，
整理得e4-6e2+1=0，
解得
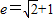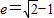或（舍去）故选C．
点评：本题考查双曲线的离心率，解题要注意时双曲线的离心率大于1．
练习册系列答案
导学教程高中新课标系列答案
小学课时特训系列答案
相关题目
的一个焦点F作它的一条渐近线的垂线FM,垂足为M并且交
轴于E，若M为EF中点，则
=___________.
的一个焦点F作一条渐近线的垂线，若垂足恰在线段
(
为原点)的垂直平分线上，则双曲线的离心率为
.
的一个焦点F作其一条渐近线的垂线，若垂足恰在线段OF（O为原点）的垂直平分线上，则双曲线的离心率为（ ）
C．
D．
的一个焦点F作一条渐近线的垂线，若垂足恰在线段
(
为原点）的垂直平分线上，则双曲线的离心率为_______
___．
的一个焦点F作一条渐近的垂线，垂足为点A，与另一条渐近线并于点B，若
，则此双曲线的离心率为（ ） 
B．
C．2 D．