题目内容
9.若实数a,b,c成等比数列,且a+b+c=4,则a+c的取值范围是[$\frac{8}{3}$,4)∪(4,8].分析 实数a,b,c成等比数列,设公比为q,则a=$\frac{b}{q}$,c=bq.又a+b+c=4,可得b=$\frac{4}{\frac{1}{q}+q+1}$.当q>0时,$0<b≤\frac{4}{3}$.当q<0时,0>b≥-4.即可得出a+c=4-b的取值范围.
解答 解:实数a,b,c成等比数列,设公比为q,
则a=$\frac{b}{q}$,c=bq.
又a+b+c=4,
∴$\frac{b}{q}$+b+bq=4,
∴b=$\frac{4q}{1+q+{q}^{2}}$=$\frac{4}{\frac{1}{q}+q+1}$.
当q>0时,$0<b≤\frac{4}{3}$,当且仅当q=1时取等号.
当q<0时,0>b≥-4,当且仅当q=-1时取等号.
∴a+c=4-b,
∴当q>0时,(a+c)∈[$\frac{8}{3}$,4);
当q<0时,(a+c)∈(4,8].
则a+c的取值范围是[$\frac{8}{3}$,4)∪(4,8].
故答案为:[$\frac{8}{3}$,4)∪(4,8].
点评 本题考查了等比数列的性质、基本不等式的性质,考查了分类讨论方法、推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
19.若复数z满足$\frac{\overline{z}}{1+i}$=2i,其中i为虚数单位,则z=( )
| A. | 2-2i | B. | -2-2i | C. | -2+2i | D. | 2+2i |
20.已知 A(-2,3)、B(4,-3)两点,则线段AB的中点坐标是( )
| A. | (3,0) | B. | (2,3) | C. | (3,3) | D. | (1,0) |
17.如图是高中课程结构图:地理所属课程是( )
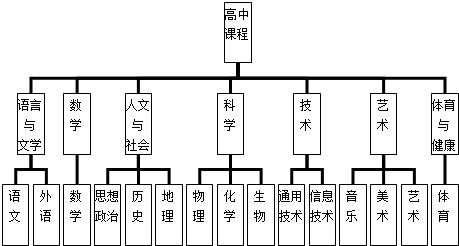

| A. | 人文与社会 | B. | 文科 | C. | 思想政治 | D. | 科学 |
1.下列函数中,为偶函数的是( )
| A. | y=x+1 | B. | y=$\frac{1}{x}$ | C. | y=x4 | D. | y=x5 |
18.定积分 $\int_{\;1}^{\;2}{4xdx}$=( )
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
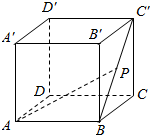 如图,ABCD-A′B′C′D′是棱长为1的正方体,点P是BC′上的动点,$\overrightarrow{BP}=λ\overrightarrow{BC'}$,则$\overrightarrow{AP}•\overrightarrow{DC}$的值是1.
如图,ABCD-A′B′C′D′是棱长为1的正方体,点P是BC′上的动点,$\overrightarrow{BP}=λ\overrightarrow{BC'}$,则$\overrightarrow{AP}•\overrightarrow{DC}$的值是1.