题目内容
已知A、B两地相距200千米,一只船从A地逆水到B地,水速为8千米/时,船在静水中的速度为v千米/时(8<v≤v0).若船每小时的燃料费与其在静水中的速度的平方成正比,当v=12千米/时时,每小时的燃料费为720元,为了使全程燃料费最省,船的实际速度为多少?
思路分析:燃料费最省,实质是求函数的最小值.
解:设每小时的燃料费为y1,比例系数为k(k>0),则y1=kv2,当v=12时,y1=720,∴720=k·122,得k=5.
设全程燃料费为y,由题意y=y1·![]() ,
,
∴y′=![]() .
.
令y′=0,∴v=16.∴当v0≥16时,v=16时全程燃料费最省;
当v0<16时,即v∈(8,v0)时y′<0,
即y在(8,v0]上为减函数,∴当v=v0时,ymin=![]()
综上,当v0≥16时,v=16千米/时全程燃料费最省,为32 000元;
当v0<16时,则v=v0时全程燃料费最省,为![]()
方法归纳 本题主要考查分类讨论的思想方法和导数的应用.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
已知A,B两地相距150km,某人开汽车以60km/h的速度从A地到达B地,在B地停留1h后再以50km/h的速度返回A地,把汽车离开A地行驶的路程x(km)表示为时间t(h)的函数表达式是( )
| A、x=60t | ||||||||||||
| B、x=60t+50t | ||||||||||||
C、x=
| ||||||||||||
D、x=
|
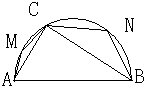 已知 A、B两地相距2R,以AB为直径作一个半圆,在半圆上取一点C,连接AC、BC,在三角形ABC内种草坪(如图),M、N分别为弧AC、弧BC的中点,在三角形AMC、三角形BNC上种花,其余是空地.设花坛的面积为S1,草坪的面积为S2,取∠ABC=θ.
已知 A、B两地相距2R,以AB为直径作一个半圆,在半圆上取一点C,连接AC、BC,在三角形ABC内种草坪(如图),M、N分别为弧AC、弧BC的中点,在三角形AMC、三角形BNC上种花,其余是空地.设花坛的面积为S1,草坪的面积为S2,取∠ABC=θ.