题目内容
【题目】已知![]() 为常数,函数
为常数,函数![]()
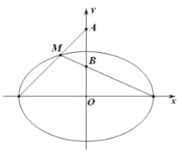
(1)过坐标原点作曲线![]() 的切线,设切点为
的切线,设切点为![]() ,求
,求![]() ;
;
(2)令![]() ,若函数
,若函数![]() 在区间
在区间![]() 上是单调减函数,求
上是单调减函数,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)求出![]() ,求出切线的点斜式方程,原点坐标代入,得到关于
,求出切线的点斜式方程,原点坐标代入,得到关于![]() 的方程,求解即可;(2)
的方程,求解即可;(2) 设
设![]() ,由
,由![]() 在
在![]() 是减函数,
是减函数,![]() ,通过研究
,通过研究![]() 的正负可判断
的正负可判断![]() 的单调性,进而可得函数
的单调性,进而可得函数![]() 的单调性,可求参数的取值范围.
的单调性,可求参数的取值范围.
(1)![]() ,
,
所以切线的斜率为![]() ,
,
切线方程为![]() 。
。
将![]() 代入得
代入得![]() ,
,
即![]() ,显然
,显然![]() 是方程的解,
是方程的解,
又![]() 在
在![]() 上是增函数,
上是增函数,
![]() 方程
方程![]() 只有唯一解,故
只有唯一解,故![]() ;
;
(2)
设![]() ,
,
![]() 在
在![]() 上是减函数,
上是减函数,
![]() ,
,
当![]() 时,即
时,即![]() 时,
时,![]() ,
,
![]() 在
在![]() 是增函数,又
是增函数,又![]() ,
,
![]() 在
在![]() 恒成立,即
恒成立,即![]() 在
在![]() 恒成立,
恒成立,
![]() 在
在![]() 上单调递减函数,所以
上单调递减函数,所以![]() ,满足题意,
,满足题意,
当![]() 时,即
时,即![]() ,
,![]() ,
,
函数![]() 有唯一的零点,设为
有唯一的零点,设为![]() ,则
,则![]() 在
在![]() 上单调递增,
上单调递增,
在![]() 单调递减,又
单调递减,又![]() ,
,
又![]() 在
在![]() 内唯一零点
内唯一零点![]() ,
,
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
从而![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增,
单调递增,
不合题意,
所以![]() 的取值范围是
的取值范围是![]() .
.

【题目】随着改革开放的不断深入,祖国不断富强,人民的生活水平逐步提高,为了进一步改善民生,2019年1月1日起我国实施了个人所得税的新政策,其政策的主要内容包括:(1)个税起征点为5000元;(2)每月应纳税所得额(含税)![]() 收入
收入![]() 个税起征点
个税起征点![]() 专项附加扣除;(3)专项附加扣除包括①赡养老人费用②子女教育费用③继续教育费用④大病医疗费用
专项附加扣除;(3)专项附加扣除包括①赡养老人费用②子女教育费用③继续教育费用④大病医疗费用![]() 等.其中前两项的扣除标准为:①赡养老人费用:每月扣除2000元②子女教育费用:每个子女每月扣除1000元.新个税政策的税率表部分内容如下:
等.其中前两项的扣除标准为:①赡养老人费用:每月扣除2000元②子女教育费用:每个子女每月扣除1000元.新个税政策的税率表部分内容如下:
级数 | 一级 | 二级 | 三级 | 四级 |
|
每月应纳税所得额(含税) | 不超过3000元的部分 | 超过3000元至12000元的部分 | 超过12000元至25000元的部分 | 超过25000元至35000元的部分 |
|
税率 | 3 | 10 | 20 | 25 |
|
(1)现有李某月收入29600元,膝下有一名子女,需要赡养老人,除此之外,无其它专项附加扣除.请问李某月应缴纳的个税金额为多少?
(2)为研究月薪为20000元的群体的纳税情况,现收集了某城市500名的公司白领的相关资料,通过整理资料可知,有一个孩子的有400人,没有孩子的有100人,有一个孩子的人中有300人需要赡养老人,没有孩子的人中有50人需要赡养老人,并且他们均不符合其它专项附加扣除(受统计的500人中,任何两人均不在一个家庭).若他们的月收入均为20000元,依据样本估计总体的思想,试估计在新个税政策下这类人群缴纳个税金额![]() 的分布列与期望.
的分布列与期望.