题目内容
在平面直角坐标系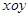 中,已知圆
中,已知圆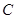 的圆心在第二象限,半径为
的圆心在第二象限,半径为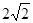 且与直线
且与直线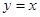 相切于原点
相切于原点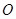 .椭圆
.椭圆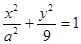 与圆
与圆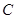 的一个交点到椭圆两焦点的距离之和为
的一个交点到椭圆两焦点的距离之和为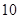 .
.
(1)求圆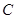 的方程;
的方程;
(2)圆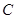 上是否存在点
上是否存在点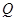 ,使
,使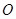 、
、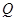 关于直线
关于直线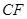
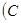 为圆心,
为圆心,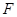 为椭圆右焦点)对称,若存在,请求出点
为椭圆右焦点)对称,若存在,请求出点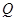 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】
解:(1)由题意知:圆心 ,半径
,半径 ,
,
圆C:
(2)由条件可知 ,椭圆
,椭圆 ,焦点
,焦点
假设存在符合条件的点,设 ,
,
则直线 ⊥
⊥ ,且线段
,且线段 中点
中点 在直线
在直线 上,
上,
又知直线CF的方程的方程为 即
即
所以由 ,
解得
,
解得 ,
,
Q的坐标为 ,该点恰在圆上。
,该点恰在圆上。
所以,圆 上存在点Q,使
上存在点Q,使 、
、 关于直线
关于直线 对称.
对称.
【解析】略

练习册系列答案
相关题目