题目内容
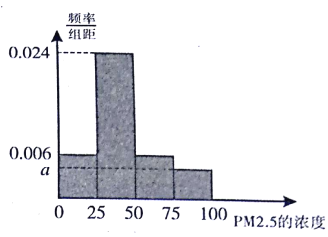
【题目】已知函数f(x)=Asin(ωx+φ),(A>0,ω>0,|φ|< ![]() )的部分图象如图所示.
)的部分图象如图所示. 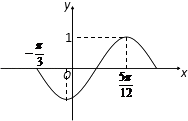
(1)求f(x)> ![]() 在x∈[0,π]上的解集;
在x∈[0,π]上的解集;
(2)设g(x)=2 ![]() cos2x+f(x),g(α)=
cos2x+f(x),g(α)= ![]() +
+ ![]() ,α∈(
,α∈( ![]() ,
, ![]() ),求sin2α的值.
),求sin2α的值.
【答案】
(1)解:由函数f(x)=Asin(ωx+φ),(A>0,ω>0,|φ|< ![]() )的部分图象知A=1,
)的部分图象知A=1,
且 ![]() =
= ![]() =
= ![]() +
+ ![]() ,
,
∴ω=2.
再根据五点法作图可得2 ![]() +φ=
+φ= ![]() ,求得φ=﹣
,求得φ=﹣ ![]() ,
,
∴f(x)=sin(2x﹣ ![]() ).
).
∵f(x)=sin(2x﹣ ![]() )>
)> ![]() ,∴
,∴ ![]() +2kπ<2x﹣
+2kπ<2x﹣ ![]() <2kπ+
<2kπ+ ![]() ,求得 kπ+
,求得 kπ+ ![]() <x<kπ+
<x<kπ+ ![]() ,k∈Z.
,k∈Z.
再根据x∈[0,π],可得 ![]() <x<
<x< ![]() ,故原不等式的解集为(
,故原不等式的解集为( ![]() ,
, ![]() )
)
(2)解:设g(x)π=2 ![]() cos2x+f(x),g(α)=2
cos2x+f(x),g(α)=2 ![]() cos2α+sin(2α﹣
cos2α+sin(2α﹣ ![]() )=
)= ![]() +
+ ![]() cos2α+
cos2α+ ![]() sin2α﹣
sin2α﹣ ![]() cos2α
cos2α
= ![]() sin2α+
sin2α+ ![]() cos2α+
cos2α+ ![]() =
= ![]() +sin(2α+
+sin(2α+ ![]() )=
)= ![]() +
+ ![]() ,
,
∴sin(2α+ ![]() )=
)= ![]() .
.
∵α∈( ![]() ,
, ![]() ),∴2α+
),∴2α+ ![]() ∈(
∈( ![]() ,
, ![]() ),∴cos(2α+
),∴cos(2α+ ![]() )=﹣
)=﹣ ![]() =﹣
=﹣ ![]() ,
,
∴sin2α=sin[(2α+ ![]() )﹣
)﹣ ![]() ]=sin(2α+
]=sin(2α+ ![]() )cos
)cos ![]() ﹣cos (2α+
﹣cos (2α+ ![]() )sin
)sin ![]() =
= ![]() ﹣(﹣
﹣(﹣ ![]() )=
)= ![]()
【解析】(1)利用函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,可得函数的解析式.(2)利用三角恒等变换求得 sin(2α+ ![]() )的值,可得cos(2α+
)的值,可得cos(2α+ ![]() )的值,再利用两角和差的正弦公式求得 sin2α=sin[(2α+
)的值,再利用两角和差的正弦公式求得 sin2α=sin[(2α+ ![]() )﹣
)﹣ ![]() ]的值.
]的值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目