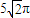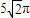题目内容
在棱锥P-ABC中,侧棱PA、PB、PC两两垂直,Q为底面△ABC内一点,若点Q到三个侧面的距离分别为3、4、5,则以线段PQ为直径的球的表面积为( )
| A.100π | B.50π | C.25π | D.5
|
根据题意:点Q到三个侧面的垂线与侧棱PA、PB、PC围成一个棱长为3、4、5的长方体,
则其外接球的直径即为PQ且为长方体的体对角线.
∴2r=
=5
∴r=
由球的表面积公式得:S=4πr2=50π
故选B.
则其外接球的直径即为PQ且为长方体的体对角线.
∴2r=
| 32+42+52 |
| 2 |
∴r=
5
| ||
| 2 |
由球的表面积公式得:S=4πr2=50π
故选B.

练习册系列答案
相关题目
在棱锥P-ABC中,侧棱PA、PB、PC两两垂直,Q为底面△ABC内一点,若点Q到三个侧面的距离分别为3、4、5,则以线段PQ为直径的球的表面积为( )
| A、100π | ||
| B、50π | ||
| C、25π | ||
D、5
|