题目内容
一车间生产A, B, C三种样式的LED节能灯,每种样式均有10W和30W两种型号,某天的产量如右表(单位:个)。按样式分层抽样的方法在这个月生产的灯泡中抽取100个,其中有A样式灯泡25个.
| 型号 | A样式 | B样式 | C样式 |
| 10W | 2000 | z | 3000 |
| 30W | 3000 | 4500 | 5000 |
(1)求z的值;
(2)用分层抽样的方法在A样式灯泡中抽取一个容量为5的样本,从这个样本中任取2个灯泡,求至少有1个10W的概率.
(1)z=2500 (2)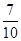
解析试题分析:解: (1).设该厂本月生产的B样式的灯泡为n个,在C样式的灯泡中抽取x个,由题意得, 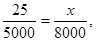 ,所以x=40. 2分
,所以x=40. 2分
则100-40-25=35,所以,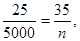 n=7000,
n=7000,
故z=2500 6分
(2) 设所抽样本中有m个10W的灯泡,
因为用分层抽样的方法在A样式灯泡中抽取一个容量为5的样本,
所以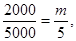 ,解得m=2 8分
,解得m=2 8分
也就是抽取了2个10W的灯泡,3个30W的灯泡,
分别记作S1,S2;B1,B2,B3,则从中任取2个的所有基本事件为
(S1, B1), (S1, B2) , (S1, B3) (S2 ,B1), (S2 ,B2), (S2 ,B3),( (S1, S2),(B1 ,B2), (B2 ,B3) ,(B1 ,B3)
共10个, 10分
其中至少有1个10W的灯泡的基本事件有7个基本事件:
(S1, B1), (S1, B2) , (S1, B3) (S2 ,B1), (S2 ,B2), (S2 ,B3),( (S1, S2),所以从中任取2个,
至少有1个10W的灯泡的概率为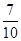 . 12分
. 12分
考点:统计和概率的综合
点评:解决的关键是理解频率和概率,并能结合古典概型概率公式求解,属于基础题。

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案为了解某班学生关注NBA是否与性别有关,对本班48人进行了问卷调查得到如下的列联表:
| | 关注NBA | 不关注NBA | 合 计 |
| 男 生 | | 6 | |
| 女 生 | 10 | | |
| 合 计 | | | 48 |
⑴请将上面列连表补充完整,并判断是否有
 的把握认为关注NBA与性别有关?
的把握认为关注NBA与性别有关?⑵现从女生中抽取2人进一步调查,设其中关注NBA的女生人数为X,求X的分布列与数学期望。
附:
 ,其中
,其中 
 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
某超市为了解顾客的购物量及结算时间等信息,安排一名员工随机收集了在该超市购物的100位顾客的相关数据,如下表所示.
| 一次购物量 | 1至4件 | 5至8件 | 9至12件 | 13至16件 | 17件及以上 |
| 顾客数(人) |  | 30 | 25 |  | 10 |
| 结算时间(分钟/人) | 1 | 1.5 | 2 | 2.5 | 3 |
(1)确定
 的值,并求顾客一次购物的结算时间
的值,并求顾客一次购物的结算时间 的分布列与数学期望;
的分布列与数学期望;(2)若某顾客到达收银台时前面恰有2位顾客需结算,且各顾客的结算相互独立,求该顾客结算前的等候时间不超过
 分钟的概率.(注:将频率视为概率)
分钟的概率.(注:将频率视为概率)  ,乙每次击中目标的概率为
,乙每次击中目标的概率为 ,两人间每次射击是否击中目标互不影响。
,两人间每次射击是否击中目标互不影响。 表示所有被取球的编号之和.
表示所有被取球的编号之和. 为坐标原点,点
为坐标原点,点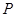 的坐标
的坐标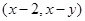
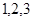 的三张卡片,现从此盒中有放回地先后抽到两张卡片的标号分别记为
的三张卡片,现从此盒中有放回地先后抽到两张卡片的标号分别记为 ,求|
,求| |的最大值,并求事件“|
|的最大值,并求事件“| ,
, ]上先后取两个数分别记为
]上先后取两个数分别记为 ,科目B每次考试合格的概率为
,科目B每次考试合格的概率为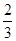 ,假设各次考试合格与否均互不影响.
,假设各次考试合格与否均互不影响.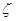 ,求随即变量
,求随即变量 ,命中得
,命中得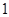 分,没有命中得
分,没有命中得 分;向乙靶射击两次,每次命中的概率为
分;向乙靶射击两次,每次命中的概率为 ,每命中一次得
,每命中一次得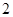 分,没有命中得
分,没有命中得 的分布列及数学期望
的分布列及数学期望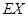 .
.