题目内容
某超市为了解顾客的购物量及结算时间等信息,安排一名员工随机收集了在该超市购物的100位顾客的相关数据,如下表所示.
| 一次购物量 | 1至4件 | 5至8件 | 9至12件 | 13至16件 | 17件及以上 |
| 顾客数(人) |  | 30 | 25 |  | 10 |
| 结算时间(分钟/人) | 1 | 1.5 | 2 | 2.5 | 3 |
(1)确定
 的值,并求顾客一次购物的结算时间
的值,并求顾客一次购物的结算时间 的分布列与数学期望;
的分布列与数学期望;(2)若某顾客到达收银台时前面恰有2位顾客需结算,且各顾客的结算相互独立,求该顾客结算前的等候时间不超过
 分钟的概率.(注:将频率视为概率)
分钟的概率.(注:将频率视为概率)
(1)
 的分布为
的分布为
X的数学期望为 X 1 1.5 2 2.5 3 P 




 .
.
(2)
解析试题分析:(1)由已知,得 所以
所以
该超市所有顾客一次购物的结算时间组成一个总体,
所以收集的100位顾客一次购物的结算时间可视为总体的一个容量随机样本,
将频率视为概率得

5分
所以 的分布为
的分布为
X的数学期望为 X 1 1.5 2 2.5 3 P 




 . 9分
. 9分
(2)记A为事件“该顾客结算前的等候时间不超过2.5分钟”, 为该顾客前面第
为该顾客前面第 位顾客的结算时间,则
位顾客的结算时间,则 .
.
由于顾客的结算相互独立,且 的分布列都与X的分布列相同,所以
的分布列都与X的分布列相同,所以
 .
.
故该顾客结算前的等候时间不超过2.5分钟的概率为 . 14分
. 14分
考点:本小题主要考查随机变量的分布列、期望和相互独立事件同时发生的概率.
点评:求解离散型随机变量问题,首先要找出随机变量的取值,其次要准确求出各个概率,可以用概率和是否为1检验求解是否正确.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
一车间生产A, B, C三种样式的LED节能灯,每种样式均有10W和30W两种型号,某天的产量如右表(单位:个)。按样式分层抽样的方法在这个月生产的灯泡中抽取100个,其中有A样式灯泡25个.
| 型号 | A样式 | B样式 | C样式 |
| 10W | 2000 | z | 3000 |
| 30W | 3000 | 4500 | 5000 |
(1)求z的值;
(2)用分层抽样的方法在A样式灯泡中抽取一个容量为5的样本,从这个样本中任取2个灯泡,求至少有1个10W的概率.
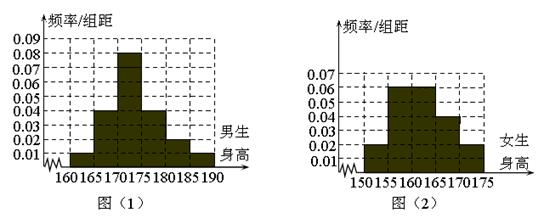 (Ⅰ)在抽取的学生中,身高不超过165cm的男、女生各有多少人?并估计男生的平均身高。
(Ⅰ)在抽取的学生中,身高不超过165cm的男、女生各有多少人?并估计男生的平均身高。 袋或
袋或 袋中.已知小球每次遇到黑色障碍物时,向左、右两边下落的概率都是
袋中.已知小球每次遇到黑色障碍物时,向左、右两边下落的概率都是 .
. ;
; 为落入
为落入 的概率和
的概率和 .
.
 ,每步上二阶的概率为
,每步上二阶的概率为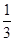 ,设该人从台阶下的平台开始出发,到达第
,设该人从台阶下的平台开始出发,到达第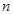 阶的概率为
阶的概率为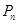 .
.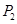 ;;
;;
 区域返券60元;停在
区域返券60元;停在 区域返券30元;停在
区域返券30元;停在 区域不返券. 例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.
区域不返券. 例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.
 (元),求随机变量
(元),求随机变量