题目内容

若|x-2|＜m成立时，|x2-4|＜1也成立，试求正数m的取值范围.

解析:设A={x||x-2|＜m,m＞0},B={x||x2-4|＜1}.?

则解B得-＜x＜-或＜x＜.??

由题意知AB,?

∴解A得2-m＜x＜m+2.?

∴

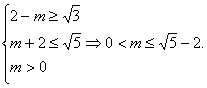
∴m的取值范围是(0,-2］.

练习册系列答案
相关题目
设函数f(x)=x3-
1
2
x2-2x+5，若对于任意x∈[-1，2]都有f（x）＜m成立，则实数m的取值范围为（　　）
A、（7，+∞）
B、（8，+∞）
C、[7，+∞）
D、（9，+∞）
已知f（x）=x3+mx2-x+2（m∈R）．
（1）如果函数f（x）的单调递减区间为（
13
，1），求函数f（x）的解析式；
（2）若f（x）的导函数为f′（x），对任意x∈（0，+∞），不等式f′（x）≥2xlnx-1恒成立，求实数m的取值范围．
f(x)=x3-
1
2
x2-2x+5，若对任意x∈[0，2]都有f（x）＜m成立，则m的取值范围为（　　）
（2009•绵阳二诊）已知f（x）=x3+mx2-x+2（m∈R）．
（1）如果函数f（x）的单调递减区间为（-
13
，1），求函数f（x）的解析式；
（2）（理）若f（x）的导函数为f′（x），对任意的x∈（0，+∞），不等式f′（x）≥2xlnx-1恒成立，求实数m的取值范围．
（文）若f（x）的导函数为f′（x），对任意的x∈（0，+∞），不等式f′（x）≥2（1-m）恒成立，求实数m的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网