题目内容
关于x的方程 的根在(1,2)内,则实数a的取值范围是
的根在(1,2)内,则实数a的取值范围是
- A.(1,2)
- B.(-1,1)
- C.(0,1)
- D.
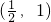
B
分析:先设函数f(x)=log (x-a)-x+2.结合根的分布得:f(1),f(2)函数值异号代入解不等式即可求出实数a的取值范围
(x-a)-x+2.结合根的分布得:f(1),f(2)函数值异号代入解不等式即可求出实数a的取值范围
解答:设:f(x)=log (x-a)-x+2
(x-a)-x+2
根据函数的单调性得在区间(1,2)内只有一个
根据零点存在性定理得:f(1),f(2)函数值异号
所以有:f(1)•f(2)=[log (1-a)-1+2]•[log
(1-a)-1+2]•[log (2-a)-2+2]<0?log
(2-a)-2+2]<0?log
 •log
•log (2-a)<0
(2-a)<0
解得: 或
或 ?-1<a<1或a不存在.
?-1<a<1或a不存在.
故:-1<a<1
故选:B.
点评:本题主要考查函数的零点与方程根的关系.解决这种问题的方法是用零点存在性定理:即函数两端点值异号.
分析:先设函数f(x)=log
 (x-a)-x+2.结合根的分布得:f(1),f(2)函数值异号代入解不等式即可求出实数a的取值范围
(x-a)-x+2.结合根的分布得:f(1),f(2)函数值异号代入解不等式即可求出实数a的取值范围解答:设:f(x)=log
 (x-a)-x+2
(x-a)-x+2根据函数的单调性得在区间(1,2)内只有一个
根据零点存在性定理得:f(1),f(2)函数值异号
所以有:f(1)•f(2)=[log
 (1-a)-1+2]•[log
(1-a)-1+2]•[log (2-a)-2+2]<0?log
(2-a)-2+2]<0?log
 •log
•log (2-a)<0
(2-a)<0解得:
 或
或 ?-1<a<1或a不存在.
?-1<a<1或a不存在.故:-1<a<1
故选:B.
点评:本题主要考查函数的零点与方程根的关系.解决这种问题的方法是用零点存在性定理:即函数两端点值异号.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
 (其中a,b为实常数)。
(其中a,b为实常数)。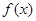 的单调区间:
的单调区间: 时,函数
时,函数 :
: 上是减函数,设关于x的方程
上是减函数,设关于x的方程 的两个非零实数根为
的两个非零实数根为 ,
, 。试问是否存在实数m,使得
。试问是否存在实数m,使得 对任意满足条件的a及t
对任意满足条件的a及t 恒成立?若存在,求m的取值范围;若不存在,请说明理由。
恒成立?若存在,求m的取值范围;若不存在,请说明理由。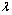 f
(x) + sinx是区间[–1,1]上的减函数.
f
(x) + sinx是区间[–1,1]上的减函数.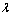 t
+ 1在x∈[–1,1]上恒成立,求t的取值范围;
t
+ 1在x∈[–1,1]上恒成立,求t的取值范围;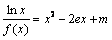 的根的个数.
的根的个数.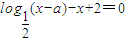 的根在(1,2)内,则实数a的取值范围是( )
的根在(1,2)内,则实数a的取值范围是( )