Question

 已知函数f (x) = ln(e^x + a)(a为常数)是实数集R上的奇函数，函数g (x) =

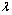f (x) + sinx是区间[–1，1]上的减函数．

（1）求a的值；

（2）若g (x)≤t² +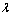t + 1在x∈[–1，1]上恒成立，求t的取值范围；

（3）讨论关于x的方程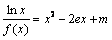的根的个数．

 

 

 

 

 

 

 

 

 

Answer 1

【答案】

 【解析】（1）由于f (x) 是R上的奇函数，f (0) = 0，故a = 0．……………………3分

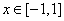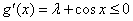（2）∵g (x)在[–1，1]上单调递减，∴时恒成立

，

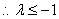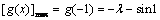
∴只要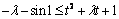

∴(t + 1)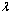+ t² + sin1 + 1≥0(其中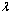≤–1)恒成立．……………………5分

令

则

∴t≤–1．………………………………………………………………………………8分

（3）由（1）知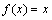．∴方程为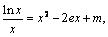

令f₁(x) =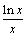，f₂(x) = x² – 2ex + m，

∵

当x∈(0，e)时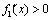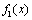，，∴在(0，e]上为增函数；

当x∈(e，+∞)时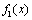，，∴在（e，+∞)上为减函数；

当x = e时．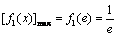

而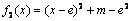

∴当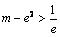时，即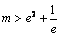时方程无解．

当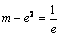时，即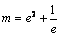时方程有一解．

当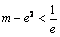时，即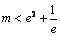时方程有二解．………………………………………13分