题目内容
设r,s,t为整数,集合{a|a=2r+2s+2t,0≤t<s<r}中的数由小到大组成数列{an}.
(1)写出数列{an}的前三项;
(2)求a36.
(1)写出数列{an}的前三项;
(2)求a36.
分析:(1)由于r,s,t为整数,且0≤t<s<r,下面对r进行分类讨论:r最小取2时,符合条件的数a有一个,当r=3时,符合条件有的数a有3个,由此求得数列{an}的前三项.
(2)同理可得r=4时,r=6时,r=7时,分别算出符合条件的数a的个数,最后利用加法原理计算即得.
(2)同理可得r=4时,r=6时,r=7时,分别算出符合条件的数a的个数,最后利用加法原理计算即得.
解答:解:(1)∵r、s、t为整数且0≤t<s<r,∴r最小取2,此时符合条件的数a有
=1;…(4分)
当r=3时,s,t 可在0,1,2中取,符合条件有的数a有
=3;…(5分)
故数列{an}的前三项为:20+21+22=7,20+21+23=11,20+22+23=13.
(2)同理,r=4时,符合条件有的数a有
=6;…(6分)
r=5时,符合条件有的数a有
=10;…(7分)
r=6时,符合条件有的数a有
=15;…(8分)
r=7时,符合条件有的数a有
=21;…(9分)
因此,a36是r=7中的最小值,即 a36=20+21+27=131.…(10分)
| C | 2 2 |
当r=3时,s,t 可在0,1,2中取,符合条件有的数a有
| C | 2 3 |
故数列{an}的前三项为:20+21+22=7,20+21+23=11,20+22+23=13.
(2)同理,r=4时,符合条件有的数a有
| C | 2 4 |
r=5时,符合条件有的数a有
| C | 2 5 |
r=6时,符合条件有的数a有
| C | 2 6 |
r=7时,符合条件有的数a有
| C | 2 7 |
因此,a36是r=7中的最小值,即 a36=20+21+27=131.…(10分)
点评:本题主要考查两个基本计数原理及数列的通项公式等基本概念,既要会合理分类,又要会合理分步,一般是先分类,后分步.

练习册系列答案
相关题目
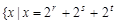 ,0≤t<s<r}中的数由小到大组成数列{an}:7,11,13,14,…,则的a36的值是
.
,0≤t<s<r}中的数由小到大组成数列{an}:7,11,13,14,…,则的a36的值是
.