题目内容
设函数
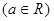
(Ⅰ)若 在点
在点 处的切线与
处的切线与 轴和直线
轴和直线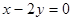 围成的三角形面积等于
围成的三角形面积等于 ,求
,求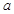 的值;
的值;
(Ⅱ)当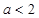 时,讨论
时,讨论 的单调性.
的单调性.
(I) 或
或 ;
;
(II) 在
在 上递增;同理
上递增;同理 在
在 和
和 上递减.
上递减.
解析试题分析:(I)∵ ,∴
,∴
又∵ ,
,
∴曲线 在点
在点 处的切线方程是:
处的切线方程是:
由 ,得
,得
则条件中三条直线所围成的三角形面积为
得 或
或 4分
4分
(II)
令 , 5分
, 5分
① 当 ,
, ,则
,则 在
在 上递增,在
上递增,在 上递减 8分
上递减 8分
②当 时,由于
时,由于 ,
,
所以 在
在 上递减,同理
上递减,同理 在
在 和
和 上是增函数 10分
上是增函数 10分
③当 时,
时,
所以, 在
在 上递增;同理
上递增;同理 在
在 和
和 上递减. 12分
上递减. 12分
考点:本题主要考查应用导数研究函数的单调性,导数的几何意义,直线方程,三角形面积计算。
点评:中档题,本题属于导数应用中的基本问题,通过求导数,确定得到切线的斜率,通过研究导数的正负,明确函数的单调性。本题函数式中含有参数a,需要运用分类讨论思想,增大了具体地难度。

练习册系列答案
相关题目
 与
与 ,如果对任意
,如果对任意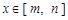 ,均有
,均有 与
与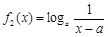 (a > 0且
(a > 0且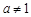 ),给定区间
),给定区间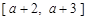 .
.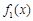 与
与 在给定区间
在给定区间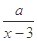 +10(x-6)2,(其中3<x<6,
+10(x-6)2,(其中3<x<6, 为常数,)已知销售价格为5元/千克时,每日可售出该商品11千克。
为常数,)已知销售价格为5元/千克时,每日可售出该商品11千克。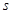 平方米,矩形一边的长为
平方米,矩形一边的长为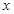 米(如图所示)
米(如图所示)
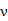 (单位:千米/小时)是车流密度
(单位:千米/小时)是车流密度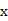 (单位:辆/千米)的函数。当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时。研究表明当
(单位:辆/千米)的函数。当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时。研究表明当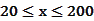 时,车流速度
时,车流速度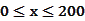 时,求函数
时,求函数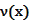 的表达式;
的表达式;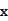 为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)
为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)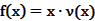 可以达到最大?并求出最大值。(精确到1辆/小时)
可以达到最大?并求出最大值。(精确到1辆/小时) 元(1≤a≤3)的管理费,预计当每件商品的售价为
元(1≤a≤3)的管理费,预计当每件商品的售价为 元(8≤x≤9)时,一年的销售量为(10-x)2万件.
元(8≤x≤9)时,一年的销售量为(10-x)2万件. 的速度顺风蔓延,消防站接到报警后立即派消防员前去,在失火后
的速度顺风蔓延,消防站接到报警后立即派消防员前去,在失火后 到达现场开始救火,已知消防队在现场每人每分钟平均可灭火
到达现场开始救火,已知消防队在现场每人每分钟平均可灭火 ,所消耗的灭火材料、劳务津贴等费用每人每分钟
,所消耗的灭火材料、劳务津贴等费用每人每分钟 元,另附加每次救火所损耗的车辆、器械和装备等费用平均每人
元,另附加每次救火所损耗的车辆、器械和装备等费用平均每人 元,而每烧毁
元,而每烧毁 森林的损失费为
森林的损失费为 元,设消防队派了
元,设消防队派了 名消防员前去救火,从到达现场开始救火到火全部扑灭共耗时
名消防员前去救火,从到达现场开始救火到火全部扑灭共耗时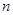
 .
.
