题目内容

在等比数列{an}中，已知a1+a2=48,a3+a4=12,求a5+a6.

思路分析一：无需单独求a5、a6的值，利用定义a2,a3,a4,a5,a6均可由a1、q表示.

解法一：设等比数列{an}的首项为a1，公比为q，由题意知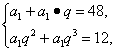解得q2=.

∴a5+a6=a1q4＋a1q5=(a1+a1q)·q4=48·（）2=3.

思路分析二：从整体上找出a1+a2与a3+a4,a5+a6的关系而求解.

解法二：由等比数列的通项公式a3+a4=a1q2+a2q2=q2(a1+a2),

a5+a6=a1q4+a2q4=q4(a1+a2),

∴(a5+a6)(a1+a2)=(a3+a4)2=q4(a1+a2),

∴a5+a6=.

练习册系列答案
相关题目
在等比数列{an}中，a4=
2
3
 ， a3+a5=
20
9
．
（1）求数列{an}的通项公式；
（2）若数列{an}的公比大于1，且bn=log3
an
2
，求数列{bn}的前n项和Sn．
在等比数列{an}中，若a1=1，公比q=2，则a12+a22+…+an2=（　　）
A、（2n-1）2
B、
1
3
（2n-1）
C、4n-1
D、
1
3
（4n-1）
在等比数列{an}中，如果a1+a3=4，a2+a4=8，那么该数列的前8项和为（　　）
在等比数列{an}中，a1=1，8a2+a5=0，数列{
1
an
}的前n项和为Sn，则S5=（　　）
在等比数列{an}中，an＞0且a2=1-a1，a4=9-a3，则a5+a6=
81
81
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网