题目内容
已知数列{an}是公差为d的等差数列,数列{bn}是公比为q的(q∈R且q≠1)的等比数列,若函数f(x)=(x-1)2,且a1=f(d-1),a3=f(d+1),b1=f(q+1),b3=f(q-1),
(1)求数列{an}和{bn}的通项公式;
(2)设数列{cn}的前n项和为Sn,对一切n∈N*,都有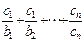 =an+1成立,求
=an+1成立,求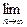
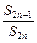

(1)求数列{an}和{bn}的通项公式;
(2)设数列{cn}的前n项和为Sn,对一切n∈N*,都有
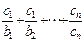 =an+1成立,求
=an+1成立,求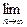
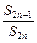

(1) an=a1+(n-1)d=2(n-1) , bn=b·qn-1=4·(-2)n-1 ,
(2)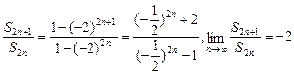
(2)
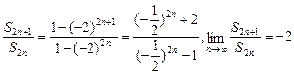
(1)∵a1=f(d-1)=(d-2)2,a3=f(d+1)=d2,
∴a3-a1=d2-(d-2)2=2d,
∵d=2,∴an=a1+(n-1)d=2(n-1);
又b1=f(q+1)=q2,b3=f(q-1)=(q-2)2,
∴ =q2,由q∈R,且q≠1,得q=-2,
=q2,由q∈R,且q≠1,得q=-2,
∴bn=b·qn-1=4·(-2)n-1
(2)令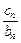 =dn,则d1+d2+…+dn=an+1,(n∈N*),
=dn,则d1+d2+…+dn=an+1,(n∈N*),
∴dn=an+1-an=2,
∴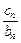 =2,即cn=2·bn=8·(-2)n-1;∴Sn=
=2,即cn=2·bn=8·(-2)n-1;∴Sn= [1-(-2)n]
[1-(-2)n]
∴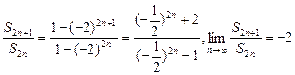
∴a3-a1=d2-(d-2)2=2d,
∵d=2,∴an=a1+(n-1)d=2(n-1);
又b1=f(q+1)=q2,b3=f(q-1)=(q-2)2,
∴
 =q2,由q∈R,且q≠1,得q=-2,
=q2,由q∈R,且q≠1,得q=-2,
∴bn=b·qn-1=4·(-2)n-1
(2)令
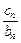 =dn,则d1+d2+…+dn=an+1,(n∈N*),
=dn,则d1+d2+…+dn=an+1,(n∈N*),∴dn=an+1-an=2,
∴
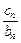 =2,即cn=2·bn=8·(-2)n-1;∴Sn=
=2,即cn=2·bn=8·(-2)n-1;∴Sn= [1-(-2)n]
[1-(-2)n]
∴
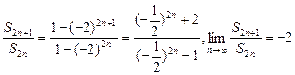

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
 满足
满足 ,若
,若 ,则
,则 _____.
_____.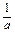 +
+ +
+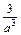 +…+
+…+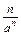 .
.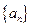 的前
的前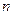 项和
项和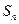 ,满足
,满足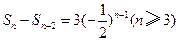 ,且
,且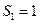 ,
,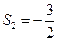 ,求数列
,求数列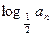 }前19项之和为_______
}前19项之和为_______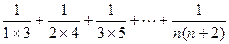 ;
;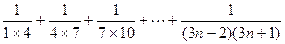 ;
; .
.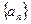 的通项公式为
的通项公式为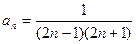 ,前
,前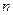 项和为
项和为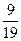 ,则
,则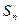 为数列
为数列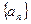 的前
的前 项和,
项和, ,则
,则