题目内容
【题目】已知
是椭圆
：
的左，右焦点．
（1）当
时，若
是椭圆上在第一象限内的一点，且
，求点的坐标；
（2）当椭圆的焦点在
轴上且焦距为2时，若直线
：
与椭圆相交于
两点，且
，求证：
的面积为定值．
【答案】见解析
【解析】（1）当
时，椭圆方程为
，则
．…………1分
设
，则
，
由
，得
，…………3分
与椭圆方程联立解得
，即点
的坐标为
．……………5分
（2）当椭圆
的焦距为2时，
，则
，
所以椭圆的方程为
．……………6分
由
得：
．…………7分
∵
，∴
，
∴
，
，
∴
，…………8分
由
，得
，∴
．
∵
．…………10分
又点
到直线
的距离
，
∴
．
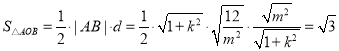即
的面积为定值．…………12分
【命题意图】本题主要考查椭圆方程与几何性质、直线与椭圆的位置关系等基础知识，意在考查逻辑思维
与推证能力、分析与解决问题的能力、运算求解能力．
练习册系列答案
相关题目
