Question

【题目】已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜ ）的部分图象如图所示．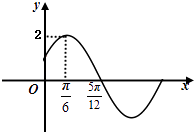

（1）求函数f（x）的解析式；
（2）令g（x）=f（﹣x﹣ ），求g（x）的单调递增区间．

Answer 1

【答案】
（1）解：由题意可知A=2，T=4（ ﹣ ）=π，ω=2，当x= 时取得最大值2，

所以 2=2sin（2x+φ），所以φ= ，

函数f（x）的解析式：f（x）=2sin（2x+ ）

（2）解：g（x）=f（﹣x﹣ ）=2sin（﹣2x﹣ ）=﹣2sin（2x+ ），

令 +2kπ≤2x+ ≤ +2kπ，k∈Z，

解得 +kπ≤x≤ +kπ，k∈Z

∴函数的单调增区间是[ +kπ， +kπ]，k∈Z．

【解析】（1）由题意求出A，T，利用周期公式求出ω，利用当x= 时取得最大
值2，求出φ，得到函数的解析式，即可．（2）先利用诱导公式得出y=﹣2sin（2x+ ）．再利用正弦函数的单调性列出不等式解出．