题目内容
已知F1,F2分别是双曲线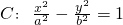 (a>0,b>0)的左,右焦点.过点F2与双曲线的一条渐近线平行的直线交双曲线于点M,且∠F1MF2=90°,则双曲线的离心率为
(a>0,b>0)的左,右焦点.过点F2与双曲线的一条渐近线平行的直线交双曲线于点M,且∠F1MF2=90°,则双曲线的离心率为
- A.

- B.

- C.2
- D.3
C
分析:先根据题意可表示出过焦点的直线与双曲线方程联立求得交点M的坐标,F1,F2的坐标,进而表示出 和
和 ,进而根据
,进而根据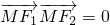 求得a和b的关系,进而求得a和c的关系,离心率可得.
求得a和b的关系,进而求得a和c的关系,离心率可得.
解答:依题意 求得x=
求得x= ,y=-
,y=-
∴ ,
,
∴
∵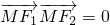
∴b2=3a2,c= =2a
=2a
∴e= =2
=2
故选C.
点评:本题主要考查了双曲线的简单性质,考查了学生综合分析问题和解决问题的能力.圆锥曲线是高考的重点每年必考,希望能够引起考生的重视.
分析:先根据题意可表示出过焦点的直线与双曲线方程联立求得交点M的坐标,F1,F2的坐标,进而表示出
 和
和 ,进而根据
,进而根据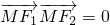 求得a和b的关系,进而求得a和c的关系,离心率可得.
求得a和b的关系,进而求得a和c的关系,离心率可得.解答:依题意
 求得x=
求得x= ,y=-
,y=-
∴
 ,
,∴

∵
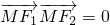
∴b2=3a2,c=
 =2a
=2a∴e=
 =2
=2故选C.
点评:本题主要考查了双曲线的简单性质,考查了学生综合分析问题和解决问题的能力.圆锥曲线是高考的重点每年必考,希望能够引起考生的重视.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目
 如图,已知F1,F2分别是椭圆C:
如图,已知F1,F2分别是椭圆C: