题目内容
(1)证明不等式: ;
;
(2)已知函数f(x)=ln(1+x)-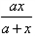 在(0,+∞)上单调递增,求实数a的取值范围;
在(0,+∞)上单调递增,求实数a的取值范围;
(3)若关于x的不等式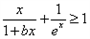 在[0,+∞)上恒成立,求实数b的最大值。
在[0,+∞)上恒成立,求实数b的最大值。
 ;
;(2)已知函数f(x)=ln(1+x)-
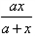 在(0,+∞)上单调递增,求实数a的取值范围;
在(0,+∞)上单调递增,求实数a的取值范围;(3)若关于x的不等式
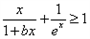 在[0,+∞)上恒成立,求实数b的最大值。
在[0,+∞)上恒成立,求实数b的最大值。解:(1)令 ,
,
则 ,
,
∴g(x)在(0,+∞)上单调递减,即g(x)<g(0),
从而 成立;
成立;
(2)由 ,
,
当x=0或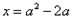 时,
时,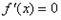 ,
,
由已知得 在(0,+∞)上恒成立,
在(0,+∞)上恒成立,
∴ ,
,
又f(x)在(0,+∞)有意义,
∴a≥0,
综上: ;
;
(3)由已知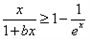 在[0,+∞)上恒成立,
在[0,+∞)上恒成立,
∵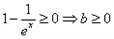 ,
,
当x>0时,易得 恒成立,
恒成立,
令 得
得 恒成立,
恒成立,
由(2)知:令a=2得:ln(1+x)> ,
,
∴ ;
;
由(1)得:
 ,
,
当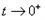 时,
时, ;
;
∴当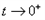 时,
时, 不大于
不大于 ;
;
∴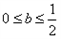 ;
;
当x=0时,b∈R,
综上: 。
。
 ,
,则
 ,
,∴g(x)在(0,+∞)上单调递减,即g(x)<g(0),
从而
 成立;
成立;(2)由
 ,
,当x=0或
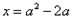 时,
时,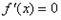 ,
,由已知得
 在(0,+∞)上恒成立,
在(0,+∞)上恒成立,∴
 ,
,又f(x)在(0,+∞)有意义,
∴a≥0,
综上:
 ;
;(3)由已知
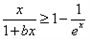 在[0,+∞)上恒成立,
在[0,+∞)上恒成立,∵
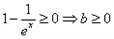 ,
,当x>0时,易得
 恒成立,
恒成立,令
 得
得 恒成立,
恒成立,由(2)知:令a=2得:ln(1+x)>
 ,
,∴
 ;
; 由(1)得:
 ,
,当
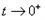 时,
时, ;
;∴当
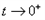 时,
时, 不大于
不大于 ;
;∴
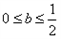 ;
;当x=0时,b∈R,
综上:
 。
。 
练习册系列答案
相关题目