题目内容
【题目】已知数列![]() 的首项
的首项![]() ,其前n项和为
,其前n项和为![]() ,对于任意正整数
,对于任意正整数![]() ,都有
,都有![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设数列![]() 满足
满足![]() .
.
①若![]() ,求证:数列
,求证:数列![]() 是等差数列;
是等差数列;
②若数列![]() 都是等比数列,求证:数列
都是等比数列,求证:数列![]() 中至多存在三项.
中至多存在三项.
【答案】(1)![]() (2)①见证明;②见证明;
(2)①见证明;②见证明;
【解析】
(1)由![]() 可得
可得![]() ,进而得到数列
,进而得到数列![]() 的通项公式;
的通项公式;
(2)①由![]() 可得
可得![]() ,利用待定系数法可得
,利用待定系数法可得![]() 从而得证;②利用反证法证明即可.
从而得证;②利用反证法证明即可.
(1)令![]() ,则由
,则由![]() ,得
,得![]()
因为![]() ,所以
,所以![]() ,
,
当![]() 时,
时,![]() ,且当n=1时,此式也成立.
,且当n=1时,此式也成立.
所以数列![]() 的通项公式为
的通项公式为![]()
(2)①【证法一】因为![]() ,
,
![]() ,
,
所以![]() .
.
由![]() 得
得![]() ,
,
所以![]() ,
,
所以![]() ,
,
所以![]() ,
,
所以![]() ,
,
所以数列![]() 是等差数列.
是等差数列.
【证法二】
因为![]()
所以![]()
所以![]() .
.
所以![]() ,
,
所以![]() ,
,
记![]()
![]() ,
,
两式相减得![]() ,
,
所以![]() ,
,
所以,当![]() 时,
时,![]() ,
,
由![]() 得
得![]() ,
,
所以,当![]() 时,
时,![]() ,当n=1时,上式也成立,
,当n=1时,上式也成立,
所以![]() ,(iii)
,(iii)
所以数列![]() 是等差数列.
是等差数列.
【证法三】
因为![]()
所以![]() ,(i)
,(i)
所以![]() ,(ii)
,(ii)
(i)-(ii)得![]() ,(iii)
,(iii)
所以![]() ,(iv)
,(iv)
(iii)-(iv)得![]() ,
,
所以![]() .
.
由![]() 知
知![]() .
.
所以![]() ,
,
所以数列![]() 是等差数列
是等差数列
②不妨设数列![]() 超过三项,令
超过三项,令![]() ,
,
由题意![]() ,则有
,则有![]() ,
,
即![]() ,
,
代入![]() ,整理得
,整理得![]() (*),
(*),
若p=q=1,则![]() ,与条件矛盾;
,与条件矛盾;
若![]() ,当n=1时,
,当n=1时,![]() ,①
,①
当n=2时,![]() ,②
,②
②÷①得,p=q,代入(*)得b=c,所以![]() ,与条件矛盾.
,与条件矛盾.
故这样的数列![]() 至多存在三项.
至多存在三项.

【题目】某高校为调查学生喜欢“应用统计”课程是否与性别有关,随机抽取了选修课程的55名学生,得到数据如下表:
喜欢统计课程 | 不喜欢统计课程 | |
男生 | 20 | 5 |
女生 | 10 | 20 |
临界值参考:
| 0.10 | 0.05 | 0.25 | 0.010 | 0.005 | 0.001 |
k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: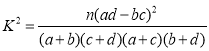 ,其中
,其中![]() )
)
参照附表,得到的正确结论是( )
A.在犯错误的概率不超过![]() 的前提下,认为“喜欢“应用统计”课程与性别有关”
的前提下,认为“喜欢“应用统计”课程与性别有关”
B.在犯错误的概率不超过![]() 的前提下,认为“喜欢“应用统计”课程与性别无关”
的前提下,认为“喜欢“应用统计”课程与性别无关”
C.有![]() 以上的把握认为“喜欢应用统计”课程与性别有关”
以上的把握认为“喜欢应用统计”课程与性别有关”
D.有![]() 以上的把握认为“喜欢“应用统计”课程与性别无关”
以上的把握认为“喜欢“应用统计”课程与性别无关”