题目内容
已知数列{an}中,a1=5且an=2an-1+2n-1(n≥2且n∈N*).
(1)证明:数列{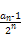
}为等差数列;
(2)求数列{an}的通项公式an.
(1)证明:∵a1=5且an=2an-1+2n-1(n≥2且n∈N*).
∴设bn=,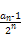
则b1=
=2.
bn+1-bn=
-
=
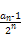
[(an+1-2an)+1]
=[(2n+1-1)+1]
=1,
由此可知,数列{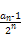}为首项是2、公差是1的等差数列.
(2)解:由(1)知,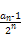=2+(n-1)×1=n+1,
an=(n+1)·2n+1.
练习册系列答案
相关题目
的公比为正数，且
=2
，
=2，则
=（ ）
B.
C.
D.2 
＝4，则
的值为 ( )．
B.
C.
D．4
,则
等于( )
(B)
(C)
(D)30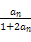
,则{an}的通项公式an= . 
,若数列{f(n)}(n∈N*)的前n项和等于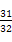
,则n等于( )