题目内容
已知直线l在x轴上的截距为1,且垂直于直线y=
x,则l的方程是( )
| 1 |
| 2 |
分析:由垂直关系可得所求直线的斜率,可设直线的方程为y=-2x+b,可解得在x轴的截距令其等于1可得b值,进而可得直线的方程.
解答:解:由题意可得直线y=
x的斜率为
,
故所求直线的斜率为-2,可设方程为y=-2x+b,
令y=0可解得x=
,由题意可知
=1,解得b=2
故可得直线的斜截式方程为y=-2x+2
故选D
| 1 |
| 2 |
| 1 |
| 2 |
故所求直线的斜率为-2,可设方程为y=-2x+b,
令y=0可解得x=
| b |
| 2 |
| b |
| 2 |
故可得直线的斜截式方程为y=-2x+2
故选D
点评:本题考查直线一般式方程与直线的垂直关系,属基础题.

练习册系列答案
相关题目
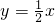 ,则l的方程是
,则l的方程是 ,则l的方程是( )
,则l的方程是( )