Question

（2010•台州一模）已知各棱长均为1的四面体ABCD中，E是AD的中点，P∈直线CE，则BP+DP的最小值为（　　）

• A．1+

  6

  3

• B．

  1+ 6 3

• C．

  1+ 3

  2

• D．

  1+ 3 2

Answer 1

分析：把平面BEC及平面CED以CE为折线展平，三角形CED是正三角形的一半，故在平面DEBC中，连接BD，与EC相交于P点，则DP+BP为最短距离，再利用余弦定理即可得出．

解答：解：由于各棱长均为1的四面体是正四面体，
把平面BEC及平面CED以CE为折线展平，三角形CED是正三角形的一半，
CE=

3

2

，DE=

1

2

，CD=1，BE=

3

2

，BC=1，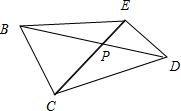
故在平面DEBC中，连接BD，与EC相交于P点，则DP+BP为最短距离，
在三角形BEC中，根据余弦定理，
cos∠BEC=

3 4 + 3 4 -1

2× 3 2 × 3 2

=

1 2

2× 3 4

=

1

3

，∴sin∠BEC=

2 2

3

，
cos∠DEB=cos（90°+∠BEC）=-sin∠BEC=-

2 2

3

，
∴BD²=BE²+DE²-2BE•DE•cos∠DEB=(

3

2

)2+(

1

2

)2-2×

3

2

×

1

2

×(-

2 2

3

)=1+

6

3

．
∴BD=

1+ 6 3

．
即BP+DP的最小值是

1+ 6 3

．
故选B．

点评：本题考查棱锥的结构特征，其中把平面BEC及平面CED以CE为折线展平得出：在平面DEBC中，连接BD，与EC相交于P点，则DP+BP为最短距离，是解题的关键．
属基础题．