题目内容
已知点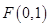 直线
直线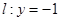 ,
,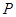 为平面上的动点,过点
为平面上的动点,过点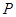 作直线
作直线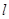 的垂线,垂足为
的垂线,垂足为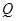 ,且
,且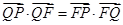 .
.
(1)求动点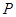 的轨迹方程;
的轨迹方程;
(2)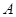 、
、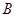 是轨迹
是轨迹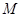 上异于坐标原点
上异于坐标原点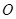 的不同两点,轨迹
的不同两点,轨迹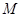 在点
在点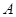 、
、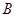 处的切线分别为
处的切线分别为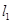 、
、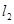 ,且
,且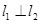 ,
,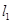 、
、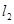 相交于点
相交于点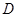 ,求点
,求点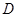 的纵坐标.
的纵坐标.
【答案】
(1)动点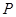 的轨迹方程为
的轨迹方程为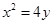 ;(2)点
;(2)点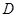 的纵坐标为
的纵坐标为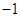 .
.
【解析】
试题分析:(1)设动点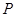 的坐标为
的坐标为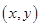 ,直接利用题中的条件列式并化简,从而求出动点
,直接利用题中的条件列式并化简,从而求出动点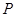 的轨迹方程;(2)先设点
的轨迹方程;(2)先设点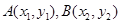 ,利用导数求出曲线
,利用导数求出曲线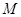 在点
在点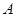 和点
和点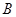 处的切线方程,并将两切线方程联立,求出交点
处的切线方程,并将两切线方程联立,求出交点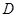 的坐标,利用两切线垂直得到
的坐标,利用两切线垂直得到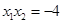 ,从而求出点
,从而求出点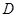 的纵坐标.
的纵坐标.
试题解析:(1)设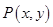 ,则
,则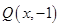 ,∵
,∵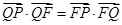 ,
,
∴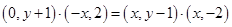 .
即
.
即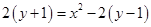 ,即
,即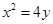 ,
,
所以动点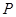 的轨迹M的方程
的轨迹M的方程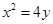 . 4分
. 4分
(2)设点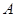 、
、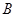 的坐标分别为
的坐标分别为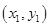 、
、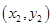 ,
,
∵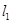 、
、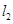 分别是抛物线
分别是抛物线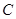 在点
在点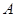 、
、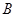 处的切线,
处的切线,
∴直线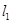 的斜率
的斜率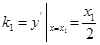 ,直线
,直线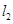 的斜率
的斜率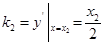 .
.
∵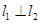 ,
,
∴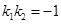 , 得
, 得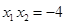 . ①
. ①
∵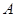 、
、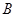 是抛物线
是抛物线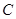 上的点,
上的点,
∴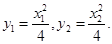
∴直线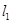 的方程为
的方程为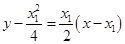 ,直线
,直线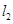 的方程为
的方程为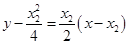 .
.
由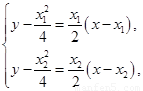 解得
解得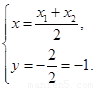
∴点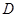 的纵坐标为
的纵坐标为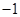 .
.
考点:1.动点的轨迹方程;2.利用导数求切线方程;3.两直线的位置关系;4.两直线的交点

练习册系列答案
相关题目
 上的点所对应的复数
上的点所对应的复数 满足
满足 ,则直线
,则直线