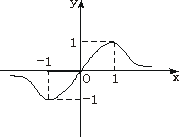
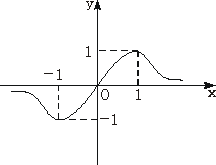
题目内容
设函数f(x)=
的图象上两点P1（x1,y1）、p2（x2,y2）,若
=
（
+
），且点P的横坐标为
.（1）求证：P点的纵坐标为定值，并求出这个定值；
（2）若Sn=
，n∈N*，求Sn：
（3）记Tn为数列{
}的前n项和，若Tn＜a（Sn+1+2）对一切n∈N*都成立.试求a的取值范围.
（1）证明：∵=（+），∴P是P1P2的中点x1+x2=1，
∴y1+y2=f（x1）+f（x2）
=
=1，
∴yp=（y1+y2）=
.
（2）解;由（1）知x1+x2=1,f(x1)+f(x2)=y1+y2=1,f(1)=2-
,
Sn=f(
)+f(
)+…+f（
）+f（
），
又Sn=f（
）+f（
）+…+f（
）+f（
）,
两式相加得
2Sn=f（1）+［f（
）+f（
）］+［f（
）+f（
）］+…［f（
）+f（
）］+f（1）=2f（1）+
=n+3-
，
∴Sn=
.
（3）解;∵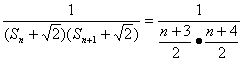
=
Tn=4[
]=
,
Tn＜a(Sn+1+
)
a＞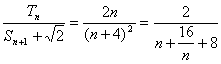
.
∵n+
，当且仅当n=4时，取“=”，
∴
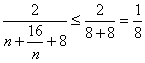，因此，a＞
.
练习册系列答案
相关题目
的图象如下图所示，则a、b、c的大小关系是
的图象如下图所示，则a、b、c的大小关系是