题目内容
已知函数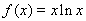 ,
,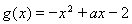 (
(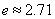 ,
, ).
).
(1)判断曲线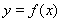 在点(1,
在点(1,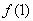 )处的切线与曲线
)处的切线与曲线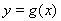 的公共点个数;
的公共点个数;
(2)当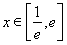 时,若函数
时,若函数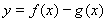 有两个零点,求
有两个零点,求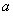 的取值范围.
的取值范围.
【答案】
(1)当△>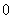 时,即
时,即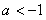 或
或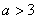 时,有两个公共点;
时,有两个公共点;
当△=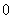 时,即
时,即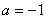 或
或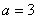 时,有一个公共点;
时,有一个公共点;
当△<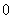 时,即
时,即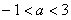 时,没有公共点 .
时,没有公共点 .
(2)当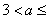
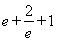 时,函数
时,函数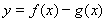 有两个零点.
有两个零点.
【解析】
试题分析:(1)求导数得切线的斜率,由直线方程的点斜式,得到曲线在点(1, )处的切线方程为
)处的切线方程为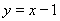 ;
;
由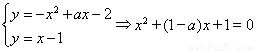 ,利用一元二次方程根的判别式讨论得解.
,利用一元二次方程根的判别式讨论得解.
(2)为讨论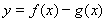 =
=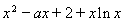 的零点,
的零点,
令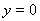 得到
得到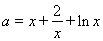 ,
,
因此可令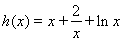 ,利用导数知识,讨论起最大值、最小值即得所求.
,利用导数知识,讨论起最大值、最小值即得所求.
试题解析:(1)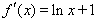 ,所以斜率
,所以斜率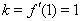 2分
2分
又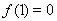 ,曲线在点(1,
,曲线在点(1, )处的切线方程为
)处的切线方程为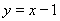 3分
3分
由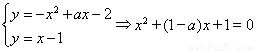 4分
4分
由△=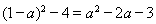 可知:
可知:
当△>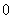 时,即
时,即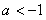 或
或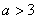 时,有两个公共点;
时,有两个公共点;
当△=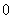 时,即
时,即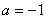 或
或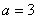 时,有一个公共点;
时,有一个公共点;
当△<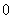 时,即
时,即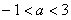 时,没有公共点 7分
时,没有公共点 7分
(2)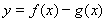 =
=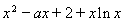 ,
,
由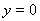 得
得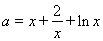 8分
8分
令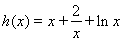 ,则
,则 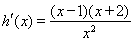
当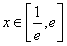 ,由
,由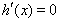 得
得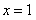 10分
10分
所以,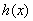 在
在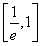 上单调递减,在
上单调递减,在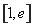 上单调递增
上单调递增
因此,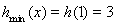 11分
11分
由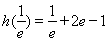 ,
,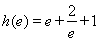 比较可知
比较可知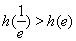
所以,当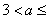
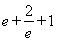 时,函数
时,函数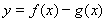 有两个零点. 14分
有两个零点. 14分
考点:导数的几何意义,应用导数研究函数的单调性、最值,直线与圆锥曲线的位置关系,转化与划归思想.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(
| ||||
B、f(x)=2sin(
| ||||
C、f(x)=2sin(2x-
| ||||
D、f(x)=2sin(2x+
|