题目内容

中心在坐标原点、焦点在x轴上的椭圆，它的离心率为，与直线x+y-1=0相交于M、N两点，若以MN为直径的圆经过坐标原点，求椭圆方程.

解：设椭圆方程+=1(a＞b＞0),

    ∵e=,∴a2=4b2，即a=2b.

    ∴椭圆方程为+=1.

    把直线方程代入化简得5x2-8x+4-4b2=0.

    设M(x1，y1)、N(x2，y2)，则

    x1+x2=，x1x2=（4-4b2）.

    ∴y1y2=（1-x1）（1-x2）

    =1-（x1+x2）+x1x2=（1-4b2）.

    由于OM⊥ON,∴x1x2+y1y2=0.

    解得b2=，a2=.

    ∴椭圆方程为x2+y2=1.


练习册系列答案
相关题目
已知椭圆C的中心在坐标原点，焦点在x轴上，椭圆C上的点到焦点距离的最大值为3，最小值为1．
（1）求椭圆C的标准方程；
（2）D为椭圆C的右顶点，设A是椭圆上异于D的一动点，作AD的垂线交椭圆与点B，求证：直线AB过定点，并求出该定点的坐标．
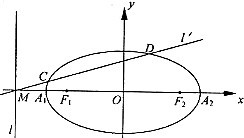精英家教网已知椭圆的中心在坐标原点，焦点F1、F2在x轴上，长轴A1A2的长为4，左准线l与x轴的交点为M，
MA1
=2
A1F1
．
（I）求椭圆的标准方程；
（Ⅱ）过点M的直线l'与椭圆交于C、D两点，若
OC
•
OD
=0，求直线l'的方程．
已知椭圆E的中心在坐标原点，焦点在x轴上，且经过A(-2，0)，B(1，
32
)两点．
（1）求椭圆E的方程；
（2）若椭圆E的左、右焦点分别是F、H，过点H的直线l：x=my+1与椭圆E交于M、N两点，则△FMN的内切圆的面积是否存在最大值？若存在，求出这个最大值及直线l的方程；若不存在，请说明理由．
（2012•房山区一模）已知椭圆G的中心在坐标原点，焦点在x轴上，一个顶点为A（0，-1），离心率为
6
3
．
（I）求椭圆G的方程；
（II）设直线y=kx+m与椭圆相交于不同的两点M，N．当|AM|=|AN|时，求m的取值范围．
（2011•延庆县一模）已知椭圆C的中心在坐标原点，焦点在x轴上，它的一个顶点B与抛物线x2=4y的焦点重合，离心率e=
2
2
．
（Ⅰ）求椭圆C的方程；
（Ⅱ）是否存在直线l与椭圆交于M、N两点，且椭圆C的右焦点F恰为△BMN的垂心（三条高所在直线的交点），若存在，求出直线l的方程，若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网