题目内容
已知函数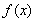 满足
满足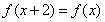 ,当
,当 时
时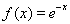 ;当
;当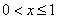 时
时 .
.
(Ⅰ)求函数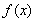 在(-1,1)上的单调区间;
在(-1,1)上的单调区间;
(Ⅱ)若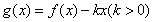 ,求函数
,求函数 在
在 上的零点个数.
上的零点个数.
【答案】
(Ⅰ) 单调递减区间为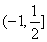 ,递增区间为
,递增区间为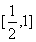 ; (Ⅱ)参考解析
; (Ⅱ)参考解析
【解析】
试题分析:(Ⅰ)因为 时,函数
时,函数 是单调递减的,
是单调递减的,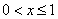 时,函数
时,函数 的图像的对称轴是
的图像的对称轴是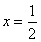 ,开口向上.所以
,开口向上.所以 递减,
递减,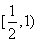 的递增.又因为当
的递增.又因为当 .所以综上可得函数的单调递减区间为
.所以综上可得函数的单调递减区间为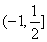 ,递增区间为
,递增区间为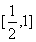 .
.
(Ⅱ)因为函数 满足
满足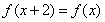 即函数的周期为2.又因为由(Ⅰ)可知(-1,1)的函数走向.所以可以知道函数在[0,3]上的图像走向.因为
即函数的周期为2.又因为由(Ⅰ)可知(-1,1)的函数走向.所以可以知道函数在[0,3]上的图像走向.因为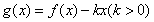 ,求函数
,求函数 在
在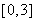 上的零点个数.即等价于求方程
上的零点个数.即等价于求方程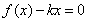 的根的个数.即等价于
的根的个数.即等价于 .即等价于函数
.即等价于函数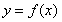 与
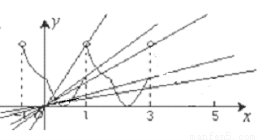
与 的图像的交点个数.所以通过如图所示即可解得结论.
的图像的交点个数.所以通过如图所示即可解得结论.
试题解析:(1)由题可知
由图可知,函数 在
在 的单调递减区间为
的单调递减区间为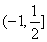 ,
,
在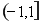 递增区间为
递增区间为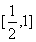 6分
6分
考察数形结合思想
(2)当 时,
时, 有1个零点 8分
有1个零点 8分
当 时,
时, 有2个零点 10分
有2个零点 10分
当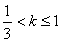 时,
时, 有3个零点 12分
有3个零点 12分
当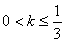 时,
时, 有4个零点 13分
有4个零点 13分
考点:1.函数的周期性.2.分段函数的性质.3.函数图像解题的思想.4.分类,归纳的思想.

练习册系列答案
相关题目
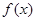 满足
满足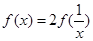 ,当
,当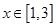 时,
时,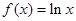 ,若在区间
,若在区间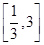 内,函数
内,函数 有三个不同零点,则实数
有三个不同零点,则实数 的取值范围是( )
的取值范围是( )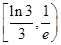 B.
B.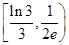 C.
C.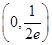 D.
D.
 满足
满足 ,且
,且 ,当
,当 时( )
时( ) B.
B. C.
C. D.以上皆不对.
D.以上皆不对. 满足:当
满足:当 时,
时, ,当
,当 时,
时, ,那么
,那么 等于( )
等于( ) B.
B. C.
C. D.
D.