Question

【题目】如图，某镇有一块空地，其中，，.当地镇政府规划将这块空地改造成一个旅游景点，拟在中间挖一个人工湖，其中M，N都在边上，且，挖出的泥土堆放在地带上形成假山，剩下的地带开设儿童游乐场.为安全起见，需在的周围安装防护网.

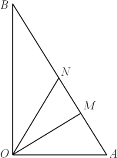
（1）当时，求防护网的总长度；

（2）为节省资金投入，人工湖的面积要尽可能小，设，问：当多大时的面积最小？最小面积是多少？

Answer 1

【答案】（1）（2）时，的面积取最小值为

【解析】

（1）证明为正三角形，可得的周长为6，即防护网的总长度为6km.
（2）在和中使用正弦定理求出，得出的面积关于的函数，利用三角函数恒等变换化简，得出面积的最小值．

解：（1）∵在中，，，

∴

又∵在中，，

∴由余弦定理得即

即

∴为正三角形，其周长为

∴防护网的总长度为

（2）由题得

在中，即（或）

在中，即

∴

（或）

又∵即

∴当且仅当即时

的面积取最小值为